|
© 2000 - 2009 Rasmus ehf |
Układ współrzędnych i równania |
Prezentacja nr
2
Równania liniowe.
Równania o
postaci y = ax + b, gdzie a i b są znanymi wielkościami, nazywane są
równaniami liniowymi, gdyż graficzna ilustracja rozwiązania w
układzie współrzędnych przedstawia linię prostą. Do
narysowania linii są potrzebne co najmniej 2
punkty, jednakże dobrze jest narysować co najmniej 3 przy
prezentowaniu rozwiązania na wykresie.
Tabela wartości:
Jeśli masz do czynienia z równaniem liniowym z dwiema
niewiadomymi, to możesz stworzyć tabelę wartości.
Tutaj mamy przykład równania liniowego: y = x + 1
Zależność między niewiadomymi musi
pozostać taka sama, ale możesz wybrać pewną
wartość x i obliczyć
odpowiadającą jej wartość y.
Tabela wartości: y = x + 1
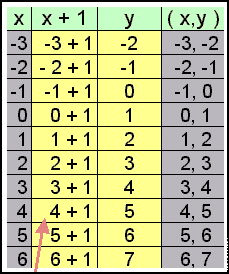
Uwaga: Możesz zdecydować jaką ilość różnych wartości chcesz obliczyć. Pamiętaj, że dobrze jest znaleźć wartości dla co najmniej 3 punktów. Jeśli te 3 punkty nie leżą na linii prostej, to znaczy, że gdzieś w twoich obliczeniach jest błąd.
Ilustracja graficzna rozwiązań równania liniowego: y = x + 1
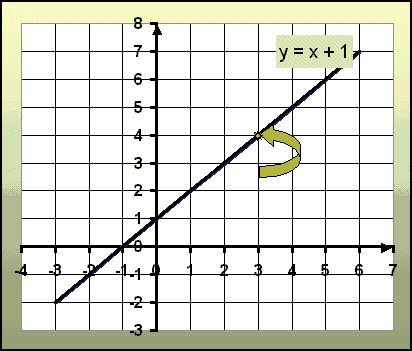
Strzałka wskazuje punkt (3,4), który jest jednym z rozwiązań znajdujących się w tabeli wartości. Kolejny punkt to (0,1), który znajduje się na przecięciu linii i osi Y. Gdy w układzie współrzędnych masz zaznaczone 2 punkty, to możesz je połączyć i otrzymać graficzną ilustrację rozwiązania równania liniowego.
Parabole
Równanie o postaci y = ax2 + b , gdzie a i b są znanymi parametrami, to równanie opisujące parabole. Potrzebujesz kilku punktów, by narysować parabolę.
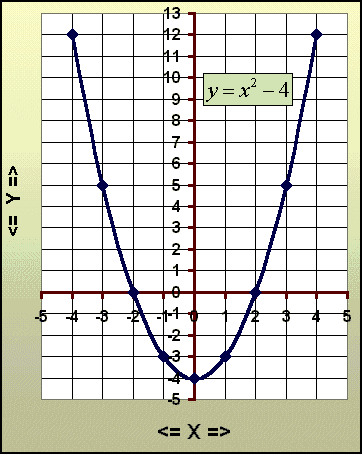
Przykład: Masz dane równanie y = x2 – 4
Oblicz kilka
wartości dla x z przedziału -4 do + 4
Stwórz tabelę wartości (patrz poniżej).
Tabela wartości dla: y = x2 - 4
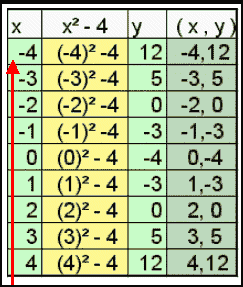
Przykład: wstaw x = -4, wtedy y = (-4)2 - 4 = 16 - 4 = 12
Zauważ, że niektóre wartości y powtarzają się. Tak jest gdyż krzywa jest symetryczna.
Wykres paraboli:
|
|
|
Wykres jest symetryczny, np. punkt (4,12) na wykresie jest odbity wzdłuż osi y (-4,12). Zwróć uwagę gdzie krzywa przecina oś y i oś x. |
Jeśli rozłożysz na czynniki równanie y = x2 – 4 to otrzymasz x2 - 4 = (x - 2)(x + 2)
Jeśli
podstawisz y = 0, to zobaczysz,
że x musi mieć
wartość +2 lub – 2, aby
równość była prawdziwa.
Dlatego współrzędne punktów
leżących na osi x to (-2,0) i (+2,0).
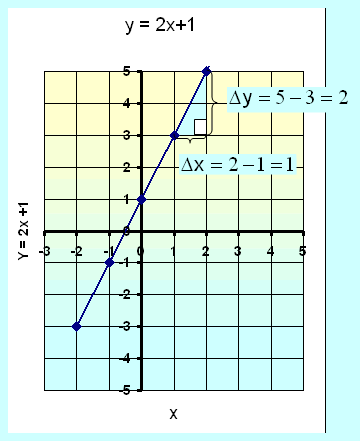
Nachylenie prostej:
Przyglądnijmy się
prostej: y = 2x + 1.
|
|
Współczynnik nachylenia prostej wynosi 2, jest to współczynnik stojący przy x. Możesz również obliczyć współczynnik nachylenia rysując trójkąt prostokątny, taki jak pokazany na diagramie, i dzieląc zmianę wartości współrzędnych y przez zmianę wartości współrzędnych x. Pionowa zmiana Δy = 5 -3 = 2 Pozioma zmiana Δx = 2 -1 = 1 Nachylenie wynosi więc 2/1 = 2 (Kiedy przenosimy się po linii od punktu 1,3 do 2,5 to wartość na osi y wzrasta o 2, a wartość na osi x o 1) |
Teraz zrób test nr 2.