Rasmus.is - Układ współrzędnych i równania

Układ współrzędnych i równania

Prezentacja nr 3

Równania i wykresy

Jeśli masz układ dwóch równań z dwiema niewiadomymi, to możesz go rozwiązać co najmniej trzema sposobami.

Sposób 1: Rysowanie prostych w układzie współrzędnych.

Przyjrzyjmy na równaniom I: y = 2x + 1 i II: y = - x + 1.

Stwórzmy tabele wartości dla każdego z równań.

y = 2x + 1
x	2x + 1	= y	x,y
-2	2·-2 + 1	-3	-2,-3
-1	2·-1 + 1	-1	-1,-1
0	2·0 + 1	1	0.1
1	2·1 + 1	3	1.3
2	2·2 + 1	5	2.5
3	2·3 + 1	7	3.7
4	2·4 + 1	9	4.9
5	2·5 + 1	11	5.11
6	2·6 + 1	13	6.13

y = -x + 1
x	-x + 1	= y	x,y
-2	-( -2) + 1	3	-2,+3
-1	-( -1) + 1	2	-1,+2
0	- 0 + 1	1	0.1
1	-(+ 1) + 1	0	..1,0
2	-(+ 2) + 1	-1	2,-1
3	-(+ 3) + 1	-2	3,-2
4	-(+ 4) + 1	-3	4,-3
5	-(+ 5) + 1	-4	5,-4
6	-(+ 6) + 1	-5	6,-5

Równanie I

Równanie II

Jeśli znajdziesz jeden lub więcej wspólnych punktów to oznacza, że proste się przecinają. Narysuj proste w układzie współrzędnych.

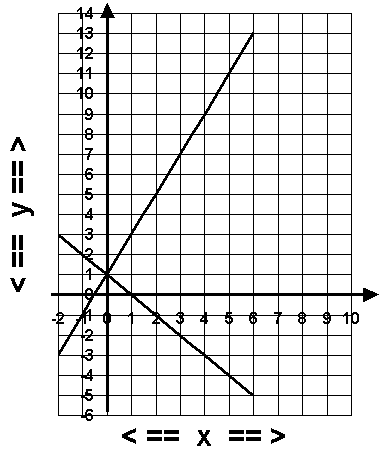
Widać tutaj, że proste przecinają się w punkcie (0,1). Zauważ, że proste te mają różne współczynniki nachylenia. Proste o różnych współczynnikach nachylenia zawsze się przecinają, podczas gdy proste o takich samych współczynnikach nachylenia są do siebie równoległe, a co za tym idzie, nigdy się nie przecinają.

Sposób 2: Dodawanie równań

Znajdowanie miejsc przecięcia się prostych to jeden ze sposobów rozwiązywania układu równań. Możemy je też rozwiązywać przez dodawanie ich wielokrotności do siebie.

I: y = 2x +1

II: y = -x + 1

Zacznij od przeniesienia x na lewą stronę równania:

I: -2x + y = + 1

II: x + y = 1

Przemnóż równanie II przez 2, aby otrzymać 2(x + y = 1) lub 2x + 2y = 2

Dodaj równania:

I: -2x + y = 1

II: 2x + 2y = 2

0 + 3y = 3 zatem y = 1 podstaw tą wartość do równania I, aby otrzymać

1 = 2x + 1 Następnie przenieś znane wartości na lewą stronę równania, aby otrzymać: +1 -1 = 2x lub 0 = 2x

Wynik to x = 0.

To jest ten sam wynik, jak uzyskany przez rysowanie prostych na wykresie.
Punkt 0,1 to jedyny wspólny punkt prostych.

Sposób 3: Podstawianie

Oba warunki są prawdziwe tylko wtedy, gdy proste się przecinają. Zatem możemy powiedzieć, że y w równaniu I i y w równaniu II są takie same w tym punkcie.

I: y = 2x +1

II: y = -x + 1

Jeśli podstawimy wyrażenie y = -x + 1 z równania II do równania I, to otrzymamy wyrażenie -x + 1 = 2x + 1.

Przenosimy znane wielkości na lewą stroną, tak aby wszystkie wartości były dodatnie.

-1 + 1 = 2x + x lub 0 = 3x Wynik to x = 0

Wstawmy otrzymaną wartość x do równania I, aby otrzymać

y = 2·x +1 = 0 + 1 = 1 Proste przecinają się w punkcie (0,1) tak jak poprzednio.

Teraz zrób test nr 3.