© 2009  Rasmus ehf

Powtórka z algebry

Powtórka z algebry

Tutaj przedstawione zostało kilka przykładowych problemów algebraicznych z którymi możesz się spotkać na egzaminie końcowym. Pod każdym zadaniem jest zamieszczony odsyłacz do rozdziału, w którym omawiany jest dany problem.  

Przykład nr 1:     Podnieś do potęgi i uprość wyrażenie.

6² + 2·2³=

36 + 2·8=

36 + 16 = 52

Zobacz_rozdział:_Kolejność_działań

Przykład nr 2:     Uprość.

y + xy +2y= 3y + xy

Zobacz_rozdział:_Wyrażenia_algebraiczne

Przykład nr 3:     Uprość.

xy +yx = 2xy

Zobacz_rozdział:_Wyrażenia_algebraiczne

Przykład nr 4:     Uprość.

a·ab = a²b

Zobacz_rozdział:_Potęgi.

Przykład nr 5:     Uprość.

Zobacz_rozdział:_Potęgi.

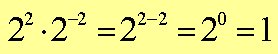
Przykład nr 6:     Rozłóż na czynniki i uprość:

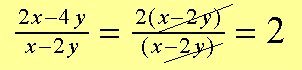
Zobacz_rozdział:_Rozkładanie_na_czynniki i Mnożenie_i_dzielenie_ułamków.

Przykład nr 7:     Rozłóż na czynniki i uprość:

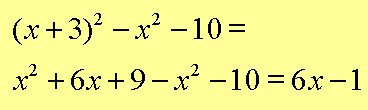
Zobacz_rozdział:_Upraszczanie_wyrażeń

Przykład nr 8:     Znajdź x:

x +14 = 30

x = 30 - 14

x = 16

Zobacz_rodział:_Równania_I

Przykład nr 9:     Znajdź x:

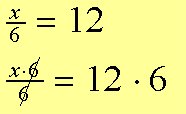
x = 72

Zobacz_rodział:_Równania_I

Przykład nr 10:     Znajdź x:

5(x + 2) = - (8 - 3x)

5x + 10 = - 8 + 3x

5x -3x = -8 -10

2x = -18

x = -9

Zobacz_rodział:_Równania_I

Przykład nr 11:    Rozwiąż równanie dla a = 3.

7a - (2a)² =

7·3 - (2·3)² =

21 - 6² =

21 - 36 = -15                  

Zobacz_rozdział:_Kolejność_działań.

Przykład nr 12:     Uprość:

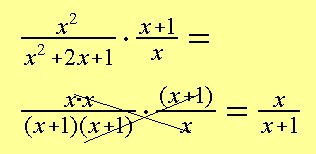
Zobacz_rozdział:_Mnożenie_i_dzielenie_ułamków i Rozkładanie_na_czynniki

Przykład nr 13:     Uprość:

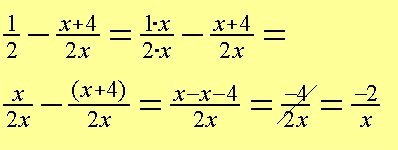
Zobacz_rozdział:_Ułamki_zwykłe_dodawanie_i_odejmowanie

Przykład nr 14:     Rozwiąż równanie:

                  

Zobacz_rozdział:_Równania_II

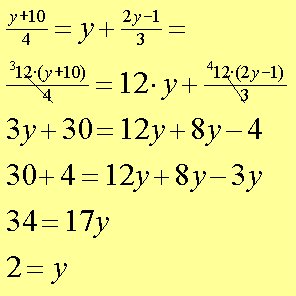
Przykład nr 15:     Rozłóż na czynniki wyrażenie i znajdź wartości x i y wiedząc, że są one liczbami całkowitymi.

Metoda nr 1:

x² - y² = 15    Zobacz_rozdział:_Rozkładanie_na_czynniki i Układ_współrzędnych

(x - y)(x + y)=3·5

Dostaniesz dwa równania

a) x - y = 3

b) x + y = 5   Dodaj do siebie równania by otrzymać:

x + x + y - y = 3 + 5

2x=8 zatem  x = 4

         
Wstaw wartość x do jednego z równań a otrzymasz:

4 + y = 5

y = 5 - 4

y =1

Metoda nr 2:

x² - y² = 15

(x - y)(x + y)=1·15

Dostaniesz dwa równania

a) x - y = 1

b) x + y = 15    Dodaj do siebie równania by otrzymać:

x + x + y - y = 1 + 15

2x=16 zatem x = 8

Wstaw wartość x do jednego z równań a otrzymasz:

8 + y = 15

y = 15 - 8

y = 7

Jeśli wykonałeś wszystkie poprzednie testy i jesteś dobrze przygotowany, to spróbuj zrobić Test końcowy! Powodzenia!