© 2009  Rasmus ehf

Statystyka

Prezentacja nr 3

Średnia, wartość środkowa, dominanta, tabela częstości, wykres słupkowy i częstość względna.

 Spójrzmy na liczbę wiadomości odebranych przez 30 użytkowników telefonów komórkowych w ciągu jednego dnia:

1,1,2,2,2,2,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,6,6,7,8,8

Stwórzmy tabelę częstości.

Liczba wiadomości

Częstość

Suma wiadomości SMS


Użytkownicy dziewięciu telefonów komórkowych otrzymali po 3 wiadomości, czyli w sumie 27 wiadomości.

  1

2

2  

  2

4

8  

  3

9

27  

  4

6

24  

  5

4

20  

  6

2

12  

  7

1

7  

  8

2

16  

Razem: ==>

30

116  

W sumie użytkownicy 30 telefonów otrzymali 116 sms'ów.

Średnia

Średnia = liczba wszystkich wiadomości / liczba użytkowników telefonów 

 

Częstość, wartość środkowa i dominanta

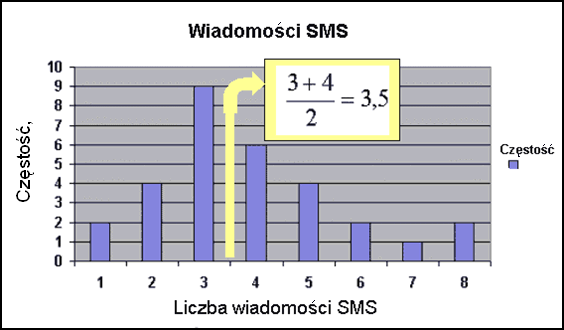
Na wykresie poniżej skala częstotliwości znajduje się na osi pionowej.
Częstość pokazuje jak dużo użytkowników otrzymało:

  • 1 wiadomość (2 użytkowników)
  • 2 wiadomości (4 użytkowników)
  • 3 wiadomości (9 użytkowników)
  • itd.

Wykres słupkowy pokazuje częstości otrzymania wiadomości SMS.

 

Jeśli spojrzymy na częstości otrzymania wiadomości, to możemy zauważyć, że:

  • (2 + 4 + 9) = 15 osób otrzymało 1, 2 lub 3 wiadomości.

  • (6 + 4 + 2 + 1 + 2) = 15 osób otrzymało 4, 5, 6, 7 lub 8 wiadomości.

  • Wartość środkowa (mediana) to liczba znajdują się między tymi dwoma grupami. 

Wartość środkowa (mediana)  wynosi 3,5 (średnia z dwóch środkowych wartości).


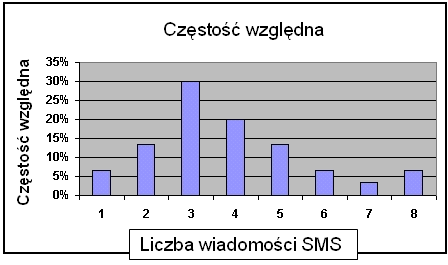
Widzimy również, że najwyższy słupek jest dla 3 wiadomości i ma częstość 9. To pokazuje, że 9 użytkowników telefonów otrzymało 3 wiadomości.

Dominanta wynosi 3, ponieważ jest to wartość, która pojawiła się najczęściej (9 razy).

 

Częstość względna    Częstość względna wyrażona w procentach

Liczba wiadomości

Częstość

Częstość względna i częstość względna wyrażona w procentach

  

  1

2

  2

4

 

 

  3

9

30% użytkowników telefonów komórkowych otrzymało 3 wiadomości sms w ciągu dnia.

  4

6

 

  5

4

 

  6

2

 

  7

1

  8

2

Suma:

30

116  

 

Wykres słupkowy częstości względnej wyrażonej w procentach.

 

 

Przećwicz powyższe przykłady, a potem zrób test nr 3.

PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.