Funktioner I
| © 2007 Rasmus ehf och Jóhann Ísak | Funktioner I |
Lektion 1 Funktioner och grafer
Exempel 1
Vi har ekvationen y = 2x + 4.
Först gör vi en tabell med värden genom att kalkylera y värdena från de x värden som vi valt. När vi ritar dessa punkter i ett koordinatsystem ser vi att de ligger på en rak linje. Vi sammanbinder dessa punkter.
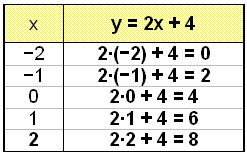 |
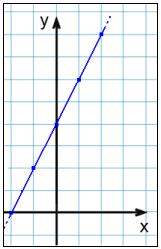 |
Detta är väldigt enkelt att göra med hjälp av en grafritande kalkylator. Om vi har en Casio väljer vi TABLE i menyn.


Vi skriver in 2x + 4 i tabellfunktionsmenyn (Table function menu) som öppnas. Y1 = 2x + 4 finns nu på skärmen.
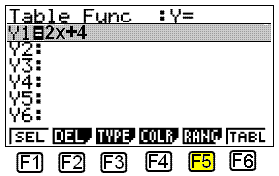
Nu måste vi bestämma vilka x-värden vi vill använda. För att göra detta väljer vi RANGE genom att trycka på F5. Följande visas på skärmen:
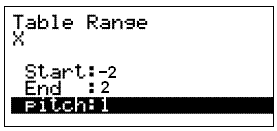
Vi väljer att börja med -2 och avsluta med 2. Pitch talar om hur många steg man vill höja x med. I vårat fall kommer vi att låta den vara 1 och sedan trycka på EXE.
Följande knapptryckningar genomför detta:
![]()
Detta tar oss tillbaka till föregående skärm där vi väljer TABLE genom att trycka på F6. Då visas tabellen med värden.
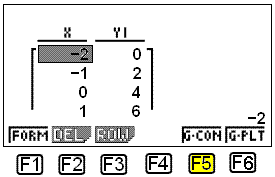
Vi kan rita grafen genom att välja G-CON ( F5 ).
Det är också möjligt att
använda programmet EXCEL till att göra tabellen med värden och rita grafen. ![]()
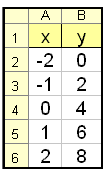
I EXCEL knappar vi in talen -2 och -1 i cellerna A2 och A3 (se EXCEL-tabellen nedan), vi kan automatiskt fylla resten av A kolumnen genom att markera A2 och A3 och sedan kopiera nedåt. Formeln i B2 är =2*A2 + 4 som kopieras ned.
| Vi kan rita grafen genom att markera talen i de två kolumnerna och sedan trycka på diagramguidsknappen (1). | |
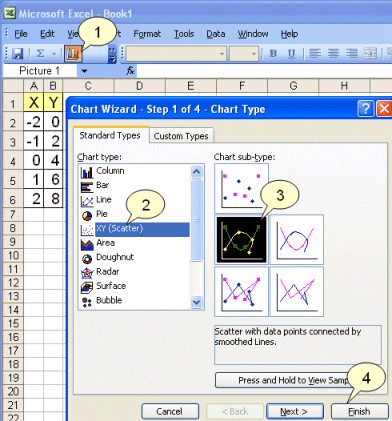 |
Vi väljer ”punkt” (2) |
| och väljer sedan en av undertyperna (3) | |
|
innan vi trycker på slutför (4). |
Vi kan sedan ändra utseendet på grafen genom att peka med musen på den punkten vi vill ändra och sedan högerklicka på musen.
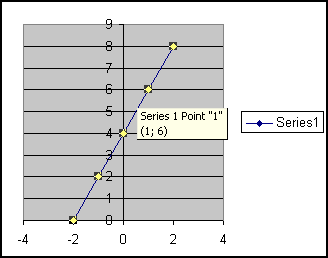
Låt oss nu titta på några fler exempel.
Exempel 2
Gör en tabell med värden och rita följande graf.
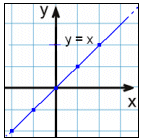
x = y |
|
 |
 |
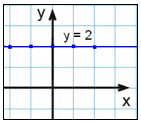
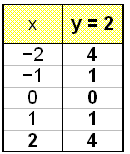
y = 2 |
|
 |
 |
y = x2 |
|
 |
 |
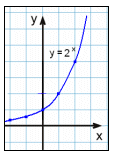
y = 2x |
|
 |
 |
Vi ska nu titta på några fler exempel som kan behandlas på samma sätt. I dessa exempel är inte formeln skriven som y =… och därför kan vi inte använda tabellfunktionen i våran räknare.
Exempel 3
x = 2
Det enda villkoret här är att x har värdet 2. När vi gör en tabell med värden måste vi alltid ha att x är lika med 2. y kan ha vilket värde som helst, vi har valt -2, -1, 0, 1 och 2. Här kan du se vår tabell med värden.
|
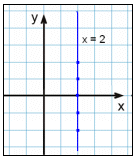 |
Resultatet är en vertikal linje genom punkten 2 på x-axeln.
Exempel 4
Härnäst ska vi undersöka relationen y2 = x.
När vi löser denna ekvation för y får vi två svar.
y = ±Med andra ord så finns det två värden på y för varje x vi väljer. Vi är dessutom begränsade till att endast välja positiva värden för x eftersom vi inte kan dra kvadratroten ur ett negativt tal. Nedan kan du se tabellen med värden och grafen.
| X | Y =±√x | 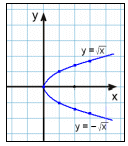 |
-1 |
Ej tillgänglig | |
0 |
0 | |
1 |
±1 | |
2 |
±√2 |
|
3 |
±√3 |
Exempel 5
Titta nu på ekvationen x2 + y2 = 4.
Lös för y:
x2 + y2 = 4
y2 = 4 − x2
![]()
Återigen får vi två y-värden för varje x-värde som vi väljer. Vi finner också att vi inte kan välja något x-värde utanför intervallet [-2, 2] därför att vi då får ett negativt tal under kvadratroten.
Tabellen med värden och grafen visas nedan.
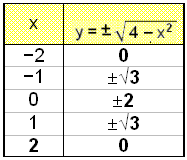 |
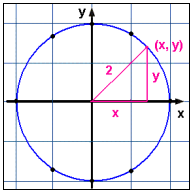 |
När vi ritar punkterna ser vi att de allihop ligger i en cirkel med sitt centrum i origo (0, 0). Cirkelns radie är 2 enheter.
Detta resultat är väldigt lättförståeligt därför att x2 + y2 = 4 egentligen är Pythagoras sats för en rätvinklig triangel med en hypotenusa utav längden 2 och de andra sidorna med längderna x och y. Dessa exempel visar att visa ekvationer med regler som sammanbinder x och y säger att det bara finns ett y-värde för varje x-värde och att visa ekvationer har mer än ett y-värde för varje x-värde.
Ekvationer som sammanbinder ett y-värde med ett x-värde är väldigt viktiga inom vetenskaperna och kallas för FUNKTIONER. Man säger att ”y är en funktion utav x” och skriver y = f(x). Detta läses som ”y är lika med f av x”
När vi tittar på grafer utav ekvationer som är funktioner ser vi att den vertikala linjen aldrig skär grafen mer än en gång.
Detta ser vi om vi tittar på graferna i exemplen som vi redan har arbetat oss igenom.
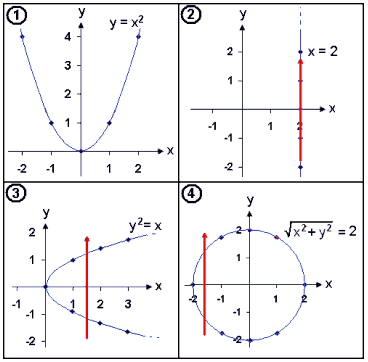
Den röda vertikala linjen skär graferna 2, 3 och 4 på två eller fler ställen vilket visar oss att detta inte är graferna av funktioner.
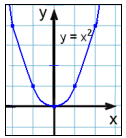
I exempel 1 så skär vilken vertikal linje vi än ritar endast grafen en gång. Detta är grafen för funktionen med ekvation y = x2 .
Vi kan både skriva denna ekvation som y = x2 och f(x) = x2 där y = f(x). Vi använder f(x) istället för y för att visa att värdet på y är beroende av värdet på x, dvs. ”är en funktion av x”.
Om vi i detta exempel väljer x = 2 så kan vi beräkna y genom formeln y = 22 = 4.
På funktionsspråk säger vi att f utav 2 är lika med 4.
Genom att använda funktionsbeteckningar kan vi skriva f(2) = 22 = 4.
Exempel 6
Med funktionen f(x) = √(2 - x) Bestäm f(0), f(1) och f(3) |
|
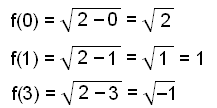 |
Vi lägger in värdena 0, 1 och 3 i ekvationen istället för x och räknar ut värdet av funktionen (y-värdet) för varje fall. |
| Detta är omöjligt | |
Vi kan lägga in bokstäver så väl som tal i funktioner. Om f(x) = x3 + x2 så är f(a) = a3 + a2 og f(a2) = a6 + a4 og f(a+1) = (a+1)3 + (a+1)2.
Exempel 7
Med funktionen f(x) = x2. Bestäm f(a), f(2a), f(a+1) og f(a+b).
f(a) = a2
f(2a) = 4a2
f(a+1) = (a+1)2 = a2 + 2a + 1
f(a+b) = (a+b)2 = a2 + 2ab + b2
Pröva
förhör 1 på funktioner I.
Kom ih åg att använda checklistan för
att hålla ordning på ditt arbete.