Mattehjälpen - Funktioner 1 - Intro 2

Funktioner I

Lektion 2 Polynomer

Följande funktioner är exempel på polynomer:

Grad	f(x)	Graf exempel:
0	f(x) = a Koefficient: a
1	f(x) = ax+b Koefficienter: a och b
2	f(x) = ax²+bx+c Koefficienter: a, b och c
3	f(x) = ax³+bx²+cx+d Koefficienter: a, b, c och d
4	f(x) = ax⁴+bx³+cx²+dx+e Koefficienter: a, b, c, d och e
Etc.

Koefficienterna a, b, c etc. är bestämda konstanta tal som avgör formen på polynomet. x är en variabel för vilken vi kan välja värden.

Den högsta exponenten utav x som förekommer i polynomet kallas för ”graden” av polynomet.

Vi skriver uttrycken med den högsta potensen på x först och därefter resten i nedgående ordning.

Om någon potens av x saknas så är det för att koefficienten utav den är noll.

Om ingen koefficient är synlig framför en av termerna så är den koefficienten 1.

Exempel 1

Hitta graden på polynomet f(x) = x⁵ − 2x³ + 4x − 5 och dess koefficienter:

Den högsta exponenten utav x är 5 så detta är ett polynom med graden 5.

x⁴ och x² saknas så deras koefficienter är 0.

x⁵ har ingen synlig koefficient så den är 1.

Vi kan se på termen utan ett x som x⁰, då alla tal med exponenten 0 är lika med 1. Nu kan vi skriva om detta polynom och lägga märke till koefficienterna.

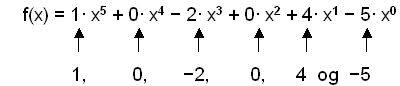Koefficienter:

Lägg märke till att ett polynom av graden 5 har 6 koefficienter. Antalet koefficienter är alltid en mer än graden på polynomet.

Exponenterna i ett polynom är alltid hela, positiva tal eller noll. (I mängden N₀). Följande funktioner är inte polynomer.

f(x) = x² + x + 1 + x⁻¹ + x⁻²	*(en negativ exponent av x)*
g(x) = x² + x + 1 + Öx	*(x är under kvadratroten)*
h(x) = x² + x + 1 + 2^x	*(x är en exponent)*
	*(x är med i nämnaren)*

Om ni tittar på graferna till polynomerna ovan så kommer ni se att ett polynom med graden 0 är en horisontell linje.

Ett första gradens polynom har en sluttande graflinje.

Ett andra gradens polynom har en graf som kallas en parabel. Den har en vändpunkt.

Ett tredje gradens är lite som två hopsatta parablar, en av dem öppnas uppåt och den andra öppnas nedåt. Det kan ha två vändpunkter.

Ett fjärde gradens liknar tre hopsatta parablar med ett högsta antal vändpunkter utav tre, o.s.v.

Allt eftersom graderna på polynomerna ökar så ökar antalet möjliga vändpunkter. Det högsta antalet vändpunkter är alltid en färre än graden på polynomet.

Det följer även att ett första gradens polynom skär x-axeln endast en gång, ett andra gradens polynom skär högst två gånger, ett tredje gradens upp till tre gånger o.s.v.

(titta på graferna igen).

Den konstanta termen (termen utan x) talar om för oss vart grafen skär y-axeln. Detta är därför att x = 0 på y-axeln och om vi sätter x = 0 i ekvationen så står vi där endast med den konstanta termen.

När f(x) = 2x³+ 3x²+ 4x + 6

f(0) = 2∙0³+ 3∙0²+ 4∙0 + 6 = 6

Punkten (0, 6) är punkten där grafen skär y-axeln.

All punkter på x-axeln har y-värdet noll så att vi kan finna vart grafen skär x-axeln genom att sätta y = 0 och lösa ekvationen för x. y = f(x) = 0.

Exempel 2

Hitta punkten där polynomet f(x) = 2x + 4 skär x- och y-axlarna. Vi kallar dessa x-interceptet och y-interceptet.

y-intercepten: är 4.	*Konstanten i formel för f(x) är 4.*
2x + 4 = 0	*Sätt f(x) = 0.*
x = ⁻⁴/₂ = −2	*Lös för x.*
Så x-intercepten är −2.

Exempel 3

Hitta skärningspunkterna för polynomet f(x) = x² − 2x på x- och y-axlarna.

y-interceptet är 0.	*Den konstanta termen är 0.*
x² − 2x = 0	*Sätt f(x) = 0.*
x (x − 2) = 0	*Faktorisera och lös för x.*
Polynomet skär x-axeln på två punkter, x= 0 och 2

Exempel 4

Hitta skärningspunkterna för polynomet f(x) = (x − 1)(x − 2)(x − 3) på x- och y-axlarna.

Om vi undersöker ekvationen så kan vi se att när vi multiplicerar ihop parenteserna så blir den konstanta termen -6.Om du inte upptäcker detta så kan du finna konstanten genom att multiplicera ihop parenteserna.

(x − 1)(x − 2)(x − 3) = (x² − 2x − x + 2)(x − 3)

= (x² −3x + 2)(x − 3)

= x³ − 3x² − 3x² + 9x + 2x − 6

= x³ − 6x² + 11x − 6

Eller ett annat enklare sätt att finna denna skärningspunkt är genom att räkna ut f(0) utan att multiplicera ihop parenteserna.

f(0) = (0 − 1)(0 − 2)(0 − 3) = −6

y – interceptet är där y = −6.

För att finna vart grafen skär x-axeln så måste vi lösa ekvationen

(x − 1)(x − 2)(x − 3) = 0

Det enda sättet som denna multiplikation kan vara noll är om en av faktorerna (parenteserna) är noll. Detta är sant för när x = 1, 2 eller 3. Därför ser vi att grafen skär x-axeln när x=1, x=2 och x=3.

Exempel 5

Ligger punkterna (1, 6) och (2, 8) på grafen utav funktionen f(x) = x² + 4x + 1.

f(1) = 1² + 4∙1 + 1	*Räkna ut värdet av f(1).*
= 1 + 4 + 1 = 6

Det följer att (1, 6) ligger på grafen.

f(2) = 2² + 4∙2 + 1

= 4 + 8 + 1 = 13

Därför ligger (2, 8) inte på grafen.

Exempel 6

Finn ekvationen på ett förstagradens polynom (en rät linje) som går genom punkterna (1, 1) och (2, 3).

Låt oss kalla funktionen f(x) = ax + b

f(1) = a∙1 + b = 1 får vi ekvationen a + b = 1	Genom att sätta in värdena (1, 1)
f(2) = a∙2 + b = 3 får vi ekvationen 2a + b = 3	Genom att sätta in värdena (2, 3)
f(2) − f(1) = (2a + b) − (a + b) = 3 − 1 = 2a + b − a − b = 2 a = 2 2 + b = 1 b = 1 − 2 = −1	Lös de simultana ekvationerna a + b = 1 2a + b = 3

Ekvationen utav polynomet (linjen) är f(x) = 2x − 1.

Exempel 7

Hitta ett andra gradens polynom (parabel) vilkens graf går genom punkterna (0, 6), (1, 0) og (3, 0).

Kalla funktionen för f(x) = ax² + bx + c och räkna ut a, b och c.

(0, 6) är y-interceptet så därför är c = 6.

(1) = a∙1² + b∙1 + 6

= a + b + 6 = 0

f(3) = a∙3² + b∙3 + 6 = 0
= 9a + 3b + 6 = 0
3a + b + 2 = 0

Förenkla ekvationen genom att dividera med 3

f(3) = f(1) = 0
       3a + b + 2 = a + b + 6
       3a − a + b − b = 6 − 2
       2a = 4
       a = 2

f(1) = 2 + b + 6 = 0
b = −2 − 6 = −8

Därför är polynomet f(x) = 2x² − 8x + 6

Pröva förhör 2 på Funktioner I.
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.