© 2008  Rasmus ehf    och Jóhann Ísak Pétursson

Faktorisering av polynom

Lektion 1

Polynomdivision och Restsatsen.

Titta på funktionen f(x) = 6x² − 9x + 3 och välj några värden på x för att göra en värdetabell. Föreställ dig att vi har haft turen att välja x = 1 och ser att f(1) = 0. 

Om x = 1 då är (x − 1) = 0 .

Faktumet att f(1) = 0 talar om för oss att (x − 1) är en faktor av f(x).

Om vi antar att (x−1) är en faktor av f(x) så kan vi även visa att
f(1) = 0:

f(x) = 6x² − 9x + 3 = (okänd faktor)(x − 1)

  f(1) = 6 − 9 + 3 = (okänd faktor)(1 − 1) = (okänd faktor)∙0

         = 0

Nu behöver vi dividera 6x² − 9x + 3 med  x − 1 för att  hitta den okända faktorn.

Nu ska vi lära oss att göra detta genom att jämföra polynomdivision med hur du lärt dig att göra med vanlig numerisk division. 

Exempel 1

Numerisk division: 

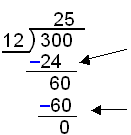Hur många gånger divideras 12 in i 30? Svaret är 2. Multiplicera nu 2×12 = 24. Subtrahera 24 from 30 och flytta ned 0. Hur många gånger divideras 12 in i 60? 5 gånger. 5×12 = 60. Subtrahera 60 from 60

Polynomdivision:

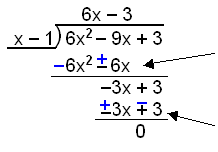Hur många gånger divideras x − 1 in i 6x2 ? Vi behöver bara fråga hur ofta x divideras in i 6x2, eller vad vi måste multiplicera x med för att få 6x2.  Svaret är 6x. Multiplicera nu 6x∙(x − 1) = 6x2 − 6x. Subtrahera 6x2 − 6x genom att ändra på tecknen framför varje term. Flytta sedan ned 3. Dividera nu x−1 in i −3x eller fråga vad du måste multiplicera x med för att få −3x?  −3×(x − 1) = −3x + 3.  Subtrahera −3x + 3 genom att ändra tecknen. Resten är is 0.

f(x) = 6x² − 9x + 3 kan nu faktoriseras helt:

f(x) =  (6x − 3)(x − 1) = 3(2x−1)(x − 1).

Exempel 2

Vi kan även faktorisera 6x² − 9x + 3 genom att använda formeln för andragradsekvationer för att lösa ekvationen 6x² − 9x + 3 = 0. 

Koefficienterna är a = 6, b = −9 och c = 3.

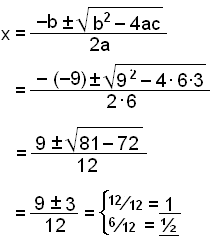
Lösningarna på ekvationen är x = 1 och x = ½ så parenteserna (x − 1) och (x − ½) måste båda vara faktorer av 6x² − 9x + 3. Vi får följande:

    6x² − 9x + 3 = 6(x − 1)(x − ½).

Vi måste ha 6 som en faktor för att få det korrekta resultatet när vi multiplicerar ihop faktorerna.

Detta exempel ger oss en regel för att faktorisera andragradsfunktioner som kan faktoriseras i två parenteser:

ax² + bx + c = a(x − r₁)(x − r₂)

Värdena r₁ och r₂  kallas RÖTTERNA till funktionen och hittas genom att lösa motsvarande andragradsekvation.

Exempel 3

Vi ska nu dvidera x³ − 6x² + 11x − 6 med x − 1 och använda resultatet till polynomet.

Att faktorisera

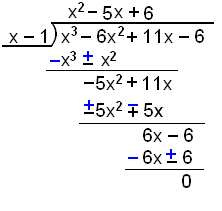	x divideras in i x3  ger x2 därför att x måste multipliceras med x2 för att få x3.   x2(x − 1) = x3 − x2. Subtrahera  x3 − x2 genom att ändra tecknen.
	Flytta ned 11x. x dividerat in i −5x2 ger −5x.  −5x(x − 1) = −5x2 + 5x.
	Subtrahera  −5x2 + 5x  genom att ändra tecknen. Flytta ned −6.  x går 6 gånger i 6x.    6(x − 1) = 6x − 6. Subtrahera.

Resten är 0 vilket betyder att (x−1) är en faktor till polynomet. Vi kan faktorisera andragradfaktorn genom utredning eller någon annan metod som vi tidigare studerat.

x³ − 6x² + 11x − 6 = (x² − 5x + 6)(x − 1) = (x − 3)(x − 2)(x − 1)

Exempel 4

Nu ska vi titta på ett svårare exempel.

Dividera the polynomet x³ − 4x + 3 med x − 1 och faktorisera sedan.

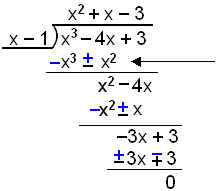I detta fall kan vi inte subtrahera   x2 och −4x, Så båda termerna förblir oförändrade.

Resten är 0 så x − 1 är en faktor. Nu återstår att faktorisera x² + x − 3. Det kan inte göras genom utredning ( att pröva sig fram ) så vi måste använda formeln för andragradsekvationens rötter (the quadratic formula)

Koefficienterna är a = 1, b = 1 och c = −3.

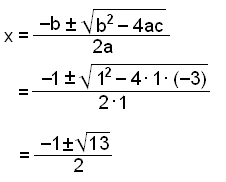
Fullt faktoriserad kommer polynomet att bli:

x³ − 4x + 3 = (x² + x − 3)(x − 1)

Exempel 5

Nu ska vi titta på ett exempel där resten inte är 0.

Dividera x³ + 4x² + x + 1 by x + 1.

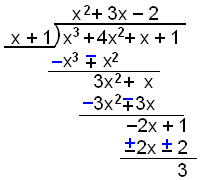
I detta exempel är resten 3.

Vi kan nu skriva om polynomet som:

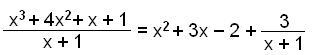
Detta sätt att skriva resultatet på är viktigt i följande:

Från detta exempel kan vi se följande generella resultat:

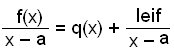rest

Där f(x) är ett polynom som divideras med (x−a) och q(x) är resultatet av divisionen (kvoten).

Om vi multiplicerar båda sidorna av denna ekvation med x − a får vi

    f(x) = q(x)(x − a) +  rest

Nu ska vi använda denna version utav f(x) för att räkna ut f(a)

    f(a) = q(a)(a − a) + rest

    f(a) = q(x)∙0 + rest

    f(a) = rest

Detta visar oss att vi kan finna resten när ett polynom divideras med x−a utan att göra någon division.

Detta kallas Restsatsen och säger följande:

  Om polynomet f(x) divideras med x − a så är resten f(a).

Exempel 6

Använd restsatsen till att finna resten när x³ + 4x² + x + 1 divideras med x + 1.

Om vi kan skriva om x + 1 som x−(−1) så kan vi använda restsatsen med a = −1.

    f(−1) = (−1)³ + 4∙(−1)² + (−1) + 1

            = −1 + 4 − 1 + 1

            = 3

O du tittar på föregående exempel, Exempel 5, kommer du se att detta överensstämmer med svaret där.

Exempel 7

Slutligen ska vi använda Restsatsen till att finna resten när x³ + 4x² + x + 1 divideras med x − 1.

Vi använder Restsatsen med a = 1 och finner resten när x³ + 4x² + x + 1 divideras med x − 1 genom att räkna ut f(1).

    f(1) = 1³ + 4∙1² + 1 + 1

          = 1 + 4 + 1 + 1

          = 7

Prova Test 1 på att Faktorisera polynom.  

Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.