Mattehjälpen - Exponenter och logaritmer

Exponenter och logaritmer.

Lektion 1 Exponenter

Vi vet att a³×a² = a×a×a × a×a = a³⁺² = a⁵. Detta exempel visar oss att när två tal, vilka är skrivna i potensform med samma bastal, multipliceras ihop så adderas indextalen ihop.

Notera: Orden potenser, exponenter och index betyder allihop samma sak.

Låt oss titta på ett andra exempel:

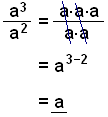
Detta visar oss att när två tal, vilka är skrivna som potenser med samma bastal divideras, så subtraheras index utav nämnaren från index utav täljaren.

Regler:

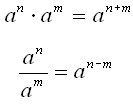
Vi ska nu titta på två speciella exempel på den andra regeln.

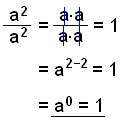
Vi använde två olika metoder för att förenkla detta uttryck så att resultatet i de båda fallen måste bli det samma. Från detta exempel så ser vi att vilket tal som helst med potensen 0 måste ha värdet 1.

Nästa exempel visar att en negativ potens är samma sak som en positiv potens under divisionslinjen.

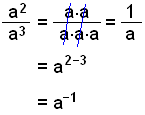
Och så har vi regeln:

Exempel 1

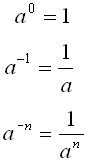
Förenkla följande uttryck genom att ge svaret med positiva index.

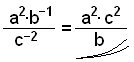Vi flyttar ner b⁻¹, vilket ändrar det till b¹= b. Flytta sedan upp c⁻² vilket ändrar den till c².

Exempel 2

Förenkla följande uttryck:

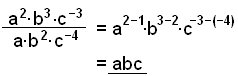Vi använder reglerna för multiplikation och division. När vi subtraherar negativa exponenter så får vi en positiv.

Exempel 3

Förenkla följande uttryck, genom att ge ditt svar med positiva exponenter:

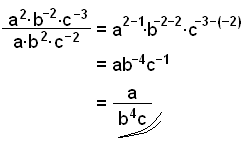
Vi ska nu undersöka vad som händer när vi höjer talen i parenteser till en potens.

(a³b)² = (a∙a∙a∙b)∙(a∙a∙a∙b) = a^3∙2 b^1∙2 = a⁶b²

Exemplet visar att alla tal (eller bokstäver) inom parenteserna är upphöjda till den givna potensen.

Regel:

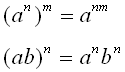
Följande exempel visar hur dessa regler används.

Exempel 4

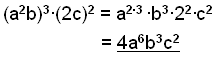Alla termer inuti parenteserna är upphöjda till potensen utanför parentesen.
(b =b¹ )

Exempel 5

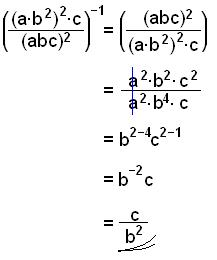Här kan vi ändra exponenten -1 till 1 genom att vända på bråket så att täljaren blir nämnaren och nämnaren blir täljaren.

Exempel 6

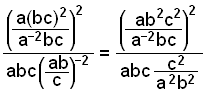	Förenkla och ta bort den innersta parentesen först.
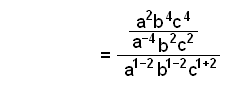	Förenkla sedan och ta bort de andra parenteserna.
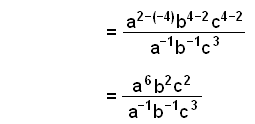	Förenkla termerna i täljaren och nämnaren.
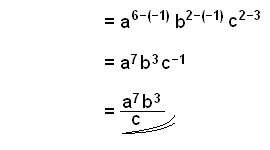	Använd nu reglerna för multiplikation och division för att förenkla hela uttrycket. Ändra slutligen alla negativa potenser till positiva.

Prova Test 1 på exponenter och logaritmer.

Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.