© 2008  Rasmus ehf   och Jóhann Ísak Pétursson

Exponenter och logaritmer.

Lektion 2     Logaritmer av basen 10.

Få tal är så enkla att arbeta med som 1, 10, 100, 1000 o.s.v. Allt vi behöver göra om vi önskar att multiplicera ihop dem är att räkna antalet nollor.

T.ex. 10∙100∙1000 = 1 000 000, totalt 6 nollor.

Vi kan också se detta om vi skriver talen som potenser av 10.

10∙100∙1000 = 10¹∙10²∙10³ = 10¹⁺²⁺³ = 10⁶ = 1000000.

För ca 400 år sedan fick matematiker idén att skriva talen som potenser av 10 skulle göra multiplikation mycket enklare. Istället för att multiplicera ihop talen skulle det endast vara nödvändigt att addera exponenterna. Innan tiden för miniräknare så var allt som gjorde kalkyler lättare mycket välkommet. 

En funktion som kallades logaritm definierades, och skrevs f(x) = log x  eller or f(x) = log x där log a är potensen som 10 måste upphöjas till för att vara samma som a.

Funktionen f(x) = log x definieras för alla positiva tal och finner potensen till vilken 10 måste upphöjas för att ge oss x. Vi kan endast finna logaritmen av positiva tal då potenser av 10 alltid är positiva.

 { x R | x > 0 }.

Vi ska nu titta på några logaritmer på en kalkylator. Denna funktion hittas på alla ingenjörsminiräknare men vi ska använda Casios grafräknare.

f(1) = log 1 = 0 därför att 10⁰ = 1

f(2) = log 2 ≈ 0,303 därför att 10^0,303 ≈ 2

f(3) = log 3 ≈ 0,477 därför att 10^0,477 ≈ 3

f(10) = log 10 = 1 därför att 10¹ = 10

f(20) = log 20 ≈ 1,303 därför att 10^1,303 ≈ 20

f(100) = log 100 = 2 därför att 10² = 100

f(1000) = log 1000 = 3 därför att 10³ = 1000

Funktionen f(x) = log x är inversen av funktionen g(x) = 10^x vilket betyder att om en funktion används på resultatet av den andra så får vi tillbaka det originella talet. Detta är samma idé som att kvadrera ett tal för att sedan ta kvadratroten ur det.

Exempel 1  Lös ekvationen

Vi tar log på bådas sidor av ekvationen.   Då funktionens log x och 10 x stryker ut varandra så har vi bara kvar x på vänster sida. Kontrollera detta resultat på din räknare.

Exempel 2

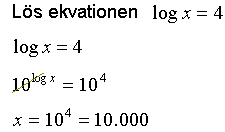Vi gör båda sidorna av ekvationen till potenser av 10. Funktionens log x och 10x stryker ut varandra och vi har endast kvar x på den vänstra sidan av ekvationen.

Logaritmer är helt enkelt exponenter (index) eller potenser och följer därför reglerna motsvarande till reglerna för index.

 Vi vet att 10^x∙10^y = 10^x+y så det betyder att om x = log a och y = log b.                              

Då är log ab = log a + log b.

Samtidigt ser vi att log( ^a/_b)= log a − log b.

Vi kan skriva log aⁿ = log a + log a + ∙ ∙ ∙ ∙ + log a (n termer) = n log a.

Detta ger oss följande logaritm regler:

Exempel 3

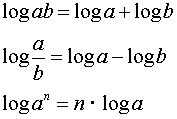
Logaritm reglerna används för att kombinera följande till en logaritm term:

a)  log a + log b + log c = log abc

b)  log a + log 2b + log 3c + log 4 = log a∙2b∙3c∙4 = log 24abc

c)  log a + log a + log a = 3 log a = log a³

d)  log 2a − log 2b = log 2 + log a − log 2 − log b = log ^a/_b

e)  ¼∙(log a + log a³) = ¼∙(log a + 3 log a) = ¼∙4 log a = log a

Exempel 4

Lös ekvationen genom att skriva vänstra sidan som en logaritm.

a) 

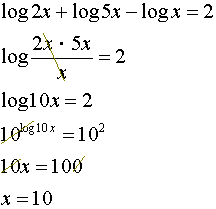
Vi börjar med att använda logaritmreglerna för att ändra den vänstra sidan från addition och subtraktion till multiplikation och division. Vi placerar sedan basen 10 på båda sidor av ekvationen. 10 och log stryker ut varandra och lämnar oss med 10x Slutligen dividerar vi med 10 för att finna x. Kontrollera detta resultat på din räknare.

b)

c)

d)

Regeln log aⁿ = n log a används för att lösa ekvationer av typen   a^x = b. 

Där exponenten är det okända värdet.

Vi tar logaritmen på båda sidor av ekvationen och använder sedan denna regel för att flytta x ned.

    a^x = b

    log a^x = log b

    x log a = log b

    x = ^{log b}/_{log a}   

Exempel 5 

Prova Test 1 på exponenter och logaritmer.

Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.