Om vi tar kvadratroten utav ett tal och sedan tar kvadraten utav resultatet, så får vi det originella talet tillbaka igen.

   T.ex. 4 = 2 og 2² = 4.

Vi kan säga att kvadratroten och kvadraten tar ut varandra. De är varandras inverser.

Om vi har ett tal med index 2 (kvadrat), att då ta ut kvadratroten innebär helt enkelt att stryka indexet 2 (detta gäller endast för positiva tal).

Vi kan därför ta vilket som helt tal i kvadrat som är under kvadratrotstecknet ut från rottecknet genom att utelämna potensen 2.

Exempel 1

Förenkla följande genom att ta ut det största möjliga värdet ur kvadratroten.

a)

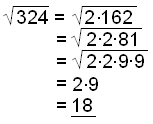Vi börjar med att faktorisera talet under rottecknet. Både 2 och 9 finns två gånger. Tar vi därför kvadratroten lämnar det oss med enbart 2 och 9. I det andra exemplet finns enbart 9 två gånger så 3 måste kvarstå under roten.

b)

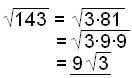
c)

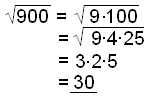
d)

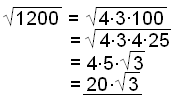
e)

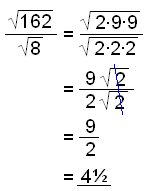
De flesta kvadratrötter är irrationella tal. Detta innebär att vi inte kan få deras exakta värden i bråk eller decimaler

P.g.a. detta får vi endast närmevärden när vi beräknar kvadratrötter på en kalkylator. Om vi lämnar kvadratroten i våra beräkningar så får vi vad som kallas exakta värden.

När man arbetar med bråk och kvadratrötter så är det brukligt att inte lämna några kvadratrötter i nämnaren.

Att förenkla för att ta bort kvadratrötter från nämnaren kallas för att ”rationalisera nämnaren”. I de enklaste exemplen så multiplicerar vi bara täljaren och nämnaren med samma kvadratrot.

Exempel 2

Rationalisera nämnarna i följande exempel:

a)

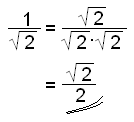Multiplicera täljaren och nämnaren med  2 . Då får vi (2)2 = 2 i nämnaren.

b)

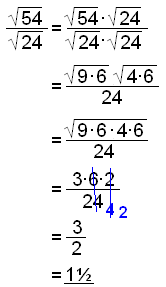När vi multiplicerar ihop två kvadratrötter så kan vi sätta båda talen under samma kvadratrotstecken.

Vi kan också lösa problemet på följande vis:

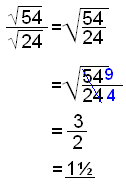Sätt båda termerna under samma kvadratrotstecken och stryk.

Om det finns två tal i nämnaren så använder vi konjugatregeln för att bli av med rötterna. (a+b) och (a−b) är konjugattermer och:

    a² − b² = (a + b)(a – b)

Vi multiplicerar täljaren och nämnaren med konjugatet av nämnaren.

d.v.s. antingen med (a − b) eller med (a + b).

Exempel 3

Rationalisera nämnaren: 

a)

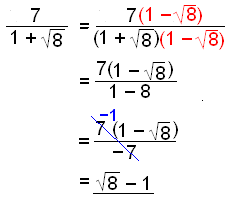Konjugatet av     är

b)

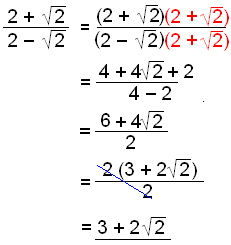
Prova Test 1 På Rötter.  

Kom ihåg att använda din checklistan för att hålla ordning på ditt arbete.