© 2008  Rasmus ehf  och Jóhann Ísak Pétursson

Rötter
Lektion 2.  Rötter och potenser.

Vi ska nu se på förhållandet mellan potenser och rötter.

Vi vet att 2∙2 = 22= 4

och därför 4 = 2.

dessutom 2∙2∙2 = 23 = 8

och därför   38 = 2.

3 före rottecknet betyder att vi tar kubikroten.

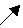Notera att när vi tar kvadratroten så sätter vi inte in 2.

Exempel:

   

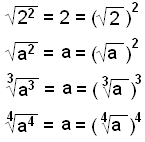
Det andra och det fjärde exemplet är bara sant om a inte är negativt.

Rötter och potenser är inversa operationer som t.ex. multiplikation och division ( om du multiplicerar med ett tal och sen dividerar med samma tal så är det som om ingenting har hänt). Man kan säga att de stryker ut varandra.

Ekvationen (a2)x = a har bara en lösning för x, vilken är x = ½, så vi drar slutsatsen att ta kvadratroten ur och höja till potensen ½ är samma operation.

Att höja till potensen ½ och att ta kvadratroten är samma operation

 

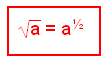Genom att använda kubikroten får vi:

 

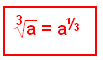Generalisering för vilken rot som helst: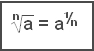 

Att ändra rötter till bråktalsexponenter och använda reglerna för exponenter kan göra många kalkyler enklare:

Exempel 1

Förenkla följande så långt som möjligt och ge svar i form av en enkel potens.

a)

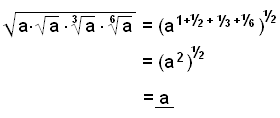Ändra alla rötter till bråktalsexponenter och samla ihop alla exponenterna under rottecknet. 

Multiplicera sedan med 1/2

 

b)

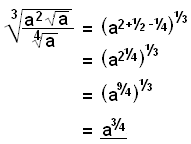
För att lösa en ekvation som:

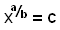
Så höjer vi båda sidorna utav ekvationen med potensen b/a.

Exempel 2

Lös följande ekvationer:

a)




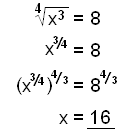När vi höjer båda sidorna till potensen 4/3 så har vi kvar x med potensen ett.

b)


Här använder vi potensen

 

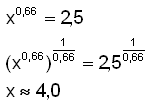Denna metod är mycket enkel att använda men vi måste se upp när vi använder den för det kan finnas tillfällen då den ger oss fel svar.

När vi höjer till jämna potenser (2, 4, 6, o.s.v.) blir alla negativa värden positiva och vi måste kontrollera att våra svar är korrekta genom att sätta in svaret i den ursprungliga ekvationen.

 

Exempel 3

Låt oss se på följande exempel:

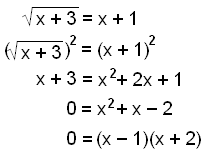
Vi får lösningarna x = 1 och x = −2. Låt oss nu undersöka dem:

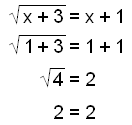
Lösningen x = 1 är korrekt.

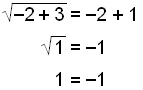
Lösningen x = −2 är inkorrekt. Vi tappade minustecknet på den vänstra sidan av ekvationen när vi kvadrerade den.

Ibland är båda lösningarna korrekta. Titta på nästa exempel.

Exempel 4

Lös för x:

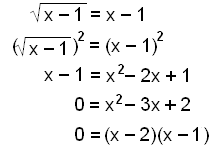
Detta ger lösningen x = 1 och x = 2.

När vi undersöker svaren får vi:

 

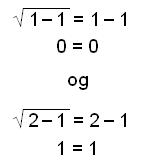
Vilka båda är korrekta.

Prova Test 2 på Rötter.  

Kom ihåg att använda din checklistan för att hålla ordning på ditt arbete.