| © 2008 Rasmus ehf och Jóhann Ísak Pétursson | Ekvationer III |
|
Vi ska nu titta på hur man löser kvadratekvationer (andragradsekvationer). Detta är samma process som att hitta grafen av en kvadratfunktion såsom
f(x) = ax2 + bx + c korsar x-axeln
Först ska vi betrakta ekvationer där koefficienterna b eller c är noll (b = 0 or c = 0).
| a) 2x2 − 8 = 0 2x2 = 8 x2 = 4 x = ±2 |
Flytta först den konstanta termen över likhetstecknet, dividera sedan båda sidorna av ekvationen med 2. Ta slutligen kvadratroten ur båda sidorna av ekvationen och kom ihåg + och -. |
| b) 2x2 + 8 = 0 2x2 = −8 x2 = −4 no solution |
I detta exemplet kan vi inte ta kvadratroten p.g.a. minustecknet. |
| a) 2x2 − 8x = 0 2x(x − 4) = 0 2x = 0 or x − 4 = 0 x = 0 or x = 4 |
Faktorisera genom att ta ut 2x ur parentesen. En av de två faktorerna måste vara noll för att multiplikationen ska kunna bli noll. |
| b) 2x2 + 8x = 0 2x(x + 4) = 0 2x = 0 or x + 4 = 0 x = 0 or x = −4 |
Återigen har vi två lösningar. Kvadratekvationer där c=0 har alltid två lösningar. |
Vi har ett svårare problem om ingen av koefficienterna a, b och c är noll.
Den enklaste typen att lösa är ekvationer som passar in i mönstret
p2 ± 2pq + p2 = (p ± q)2
| a) x2 + 2x + 1 = 0 (x + 1)2 = 0 (x + 1) = 0 x = −1 |
Detta passar exakt in i mönstret ovan. |
| b) 2x2 − 8x + 8 = 0 2(x2 −4x + 4) = 0 2(x – 2)2 = 0 (x − 2) = 0 x = 2 |
Om vi tar 2 utanför parentesen så passar även detta in i mönstret. |
Ibland kan vi faktorisera ekvationen utan att räkna (gissa faktorerna), och sedan hitta värdet på x som gör att varje faktor blir noll.
Exempel 4
Lös ekvationen x2 − 5x + 6 = 0
x2 − 5x + 6 = 0
(x − 2)(x − 3) = 0
x = 2 or x = 3
Exempel 5
Lös ekvationen x2 − 4x − 5 = 0. x2 − 4x − 5 = 0 x2 − 4x + 22 − 22 − 5 = 0 (x2 − 4x + 4) − 9 = 0 |
Här kompletterar vi kvadraten genom att lägga till (och sedan subtrahera) halva koefficienten av b i kvadrat. Vi kan använda regeln p2± 2pq + q2 = (p ± q)2 |
|
(x − 2)2 − 9 = 0 |
Resultatet är i formen (x + r)2 + s |
x − 2 = ±3 x = 2 ± 3 x = 5 or x = −1 |
vilken introducerades i den 3:e lektionen av Funktioner 1 |
Exempel 6
Lös ekvationen 3x2 − 24x + 21 = 0
3(x2 − 8x) + 21 = 0
3(x2 − 8x + 42) − 3∙42 + 21 = 0
3(x − 4)2 − 48 + 21 = 0
3(x − 4)2 = 27
(x − 4)2 = 9
x − 4 = ±3
x = 4 + 3 = 7 or x = 4 − 3 = 1
Exempel 7
Vi ska nu hitta en formel vilken vi kan använda till att lösa vilken andragradsekvation som helst utav formen ax2 + bx + c = 0
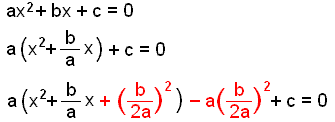 |
Flytta a utanför parentesen. Lägg till halva koefficienten av x i kvadrat. Subtrahera samma tal och kom ihåg att multiplicera med a. |
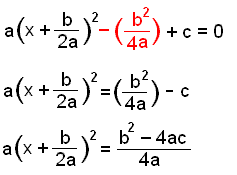 |
Skriv de första tre termerna av ekvationen som en parentes i kvadrat
Flytta de andra två termerna över likhetstecknet och hitta den gemensamma nämnaren. |
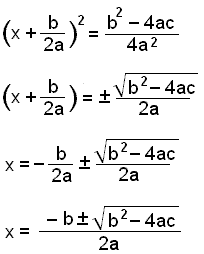 |
Ta nu kvadratroten ur båda sidor av ekvationen och kom ihåg + och -.
Lös slutligen för x genom att flytta termen in i parentesen över likhetstecknet. |
Algebran i detta bevis är ganska komplicerad men när vi väl har hittat formeln så måste vi inte gå igenom processen igen och vi kan använda den till att lösa vilken kvadratekvation som helst.
Detta är formeln som vi använder för att lösa ekvationen ax2 + bx + c = 0
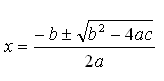 |
Detta är en av de mest välkända och mest välanvända formlerna inom matematik.
Exempel 8
Vi ska nu använda denna formel för att lösa ekvationen
2x2 − 10x + 8 = 0Koefficienterna är: a = 2
b = −10
c = 8
Sätt dessa tal för a, b och c in i formeln
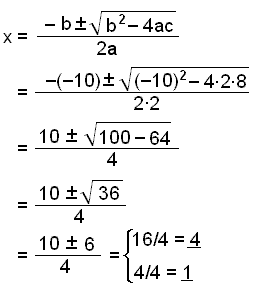
Exempel 9
Lös ekvationen x2 − 3x + 6 = 0
Koefficienterna är a = 1, b = −3 och c = 6.
De sätts in i formeln.
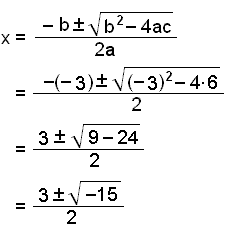
I detta exemplet är talet under kvadratroten negativt så ekvationen har ingen lösning.
Exempel10
Vi kan lösa kvadratekvationer genom att använda en grafräknare.

Detta är hur man löser ekvationen 2x2 − 10x + 8 = 0 genom att använda en grafräknare.
Välj först „EQUA“ i menyn.
Vi får då:
Välj nu „Polynomial“ med F2 .

Vi löser kvadratekvationen genom att välja 2 (tryck på F1). Vi kan även lösa tredjegradsekvationer genom att välja 3. Detta är skärmen som vi ser:
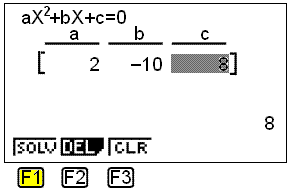
Vi sätter in värdena a = 2, b = −10 och c = 8 genom att trycka på exe mellan varje värde.
Följande visar ordningsföljden utav handlingar:
![]()
Välj slutligen SOLV genom att trycka F1. Lösningarna 4 och 1 visar sig på följande skärm:
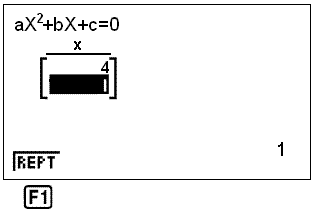
Exempel 11
Låt oss se hur räknaren tar itu med en ekvation som inte har någon lösning. Titta på ekvationen x2 − 3x + 6 = 0. Vi trycker in värdena a = 1, b = −3 och c = 6. Räknaren ger oss följande lösning:
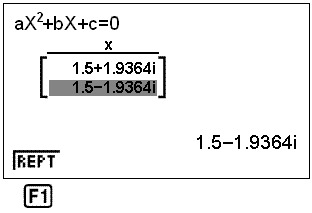
Detta betyder att svaret är vad som är känt som ett Komplext tal inte ett REELLT tal. Ingen REELL tals lösning existerar.
Exempel 12
Vi ska nu se hur vi kan använda EXCEL till att lösa en kvadratekvation. Vi ska använda EXCEL till att lösa ekvationen 2x2 − 10x + 8 = 0. Skriv a, b och c i cellerna A3, B3 och C3.
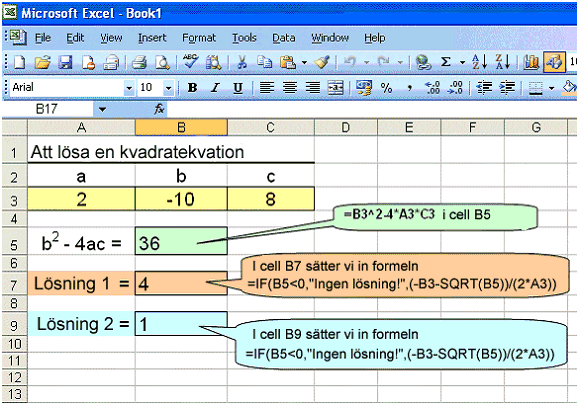
Vi skriver formeln
=B3^2-4*A3*C3 i cell B5
I cell B7 sätter vi in formeln
=IF(B5<0,"Ingen lösning!",(-B3+SQRT(B5))/(2*A3))
I cell B9 sätter vi in formeln
=IF(B5<0,"Ingen lösning!",(-B3-SQRT(B5))/(2*A3))
Om vi använder detta program till att lösa en ekvation som bara har en lösning, t.ex. x2 − 2x + 1 = 0, så får vi samma svar två gånger.

Om ekvationen inte har någon lösning, såsom ekvationen x2 − 3x + 6 = 0 så ger EXCEL oss detta:

Prova Test 1 på Ekvationer III.
Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.