© 2008  Rasmus ehf  og Jóhann Ísak

Trianglar

Lektion 2

   Några viktiga kännetecken

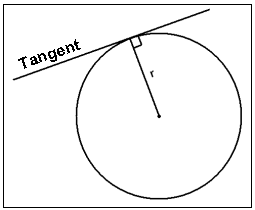
En rak linje som genomskär en cirkel endast en gång (nuddar cirkeln) kallas för en tangent till cirkeln. Vinkeln mellan radien och en tangent vid skärningspunkten är alltid 90°.

En rak linje som delar en vinkel i två likadana delar kallas för vinkelns bisektris. Alla punkter på vinkelns bisektris är alla på samma avstånd från armarna eller sidorna till den uppdelade vinkeln. En cirkel, ritad så att sidorna av en vinkel är tangenter till cirkeln, har sin center i vinkelns bisektris.

I diagrammet ovan så är linjen från V genom O vinkelns bisektris till vinkeln V. Sträckorna VA och VB är av likadana längder och är vinkelräta till AO respektive BO.

Exempel 1

I diagrammet nedan är vinkeln V = 40° och sträckorna VA och VB är 40 cm. Finn vinkeln AOB, märkt x, och cirkelns radie.

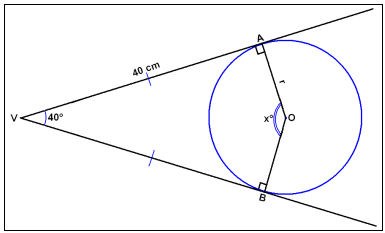
VAOB är fyrsidig och därför är summan av vinklarna 360°. Vi vet vad tre av vinklarna är och kan därför beräkna den fjärde.

   x° = 360° − 90° − 40° − 90° = 140°

Om vi ritar vinkelns bisektris till VO så får vi en rätvinklig triangel med vinklar på  20°, 90° and 70°.  Genom att använda trigonometri får vi:

     tan 20° = ^r/₄₀

                 r = 40∙tan 20° ≈ 14,6 cm

En vinkels bisektris delar den sidan av triangeln som är motsatt till vinkeln i samma förhållande som sträckorna vilka är närliggande till vinkeln.

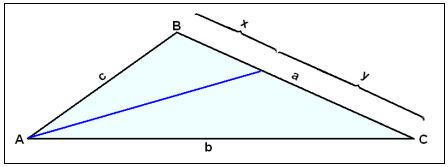
Vinkel bisektrisen till vinkeln A delar sidan a i förhållandet  ^c/_b. Om vi kallar dessa delar x och y så gäller följande regler:

Exempel 2

Triangeln ABC har följande mått:

   a = 30 cm, b = 40 cm och c = 20 cm.

Vinkel bisektrisen till vinkeln A delar sidan a i två delar. Räkna ut längden på dessa delar. Vi använder samma beteckningssätt som i regeln ovan.

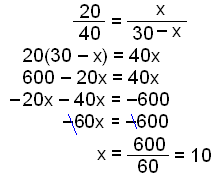
Sidan a är delad i bitar med längderna  10 cm och 30 − 10 = 20 cm.

Varje triangel har en punkt som är på samma avstånd från alla tre sidorna av triangeln. Detta är punkten där alla vinkelbisektriserna till triangeln korsar varandra. Genom att använda denna punkt som center så kan vi rita en cirkel som nuddar alla tre sidorna av triangeln. Detta kallas den inskrivna cirkeln av triangeln.

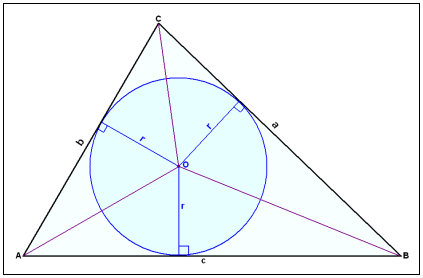
Vi kan se från vårt diagram ovan att vinkelbisektriserna AO, BO och CO delar triangeln i tre mindre trianglar där varje av dessa har höjden r. Deras areor är ½×a×r, ½×b×r and ½×c×r. Den totala arean, dvs. arean av triangeln ABC, är därför:

  Area F = ½∙a∙r + ½∙b∙r + ½∙c∙r = ½∙r(a + b + c)

Omkretsen på cirkeln, låt oss kalla den u, är a+ b+ c vilket betyder att vi kan skriva formeln för arean på triangeln enligt följande:

Det finns en andra punkt, som kan vara antingen innanför eller utanför triangeln, som är på samma avstånd från alla vinklar på triangeln. Denna punkt är där alla tre mittpunktsnormaler till triangeln korsar varandra. Detta är därför att punkter på mittpunktsnormalen är på samma avstånd från vinklar som utgör sluten på sidor som de tudelar.

Denna punkt formar centret av cirkeln som kan ritas genom alla punkter på triangeln. Den kallas för den omskrivna cirkeln av triangeln.

Diagrammet ovan visar triangeln ABC med dess omskrivna cirkel. Två rätvinkliga trianglar har ritats i diagrammet. Triangeln ACE formas genom att rita höjden h från vinkeln C till sidan c. Triangeln BCD finnes genom att rita diametern på cirkeln från C genom centret O till en punkt D på cirkeln. Trianglarna ACE och BCD är likformiga då de båda är rätvinkliga trianglar och vinkeln A = vinkeln D. (båda omfattar bågen CB) Därför gäller följande förhållande:

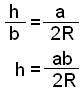
Genom att sätta detta värde för h in i formeln för arean F av en triangel, F = ½×c×h så får vi följande resultat:

Vi kan även använda följande:

Vilket leder till regeln:

Om vi löser för h och sätter in värdet h = b×sin A in i formeln för arean F = ½×c×h så erhåller vi regeln för triangelns area:

 F = ½∙b∙c∙sin A

Exempel 3

En triangel har sidor med längderna 17 cm, 17 cm och 16 cm.

a) Finn triangelns area.

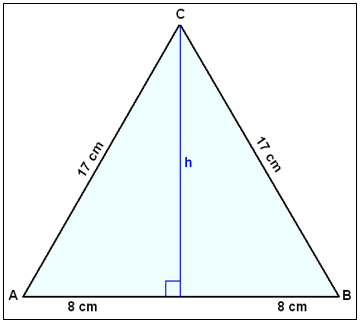
Använd Pytagoras sats för att finna höjden h.

  h² + 8² = 17²

           h² = 289 − 64 = 225

            h = 15 cm

Nu kan vi beräkna arean F.

   F = ½∙16∙15 = 120 cm² 

b) Finn radien på den inskrivna cirkeln.

Omkretsen på triangeln u = 17 + 17 + 16 = 50 cm.

   Area  F = 120 = ½∙r∙50

           r =^120∙2/₅₀ = 4,8 cm

c) Finn radien på den omskrivna cirkeln.

    Area F = 120 = 17∙17∙16/4R

        480R = 17∙17∙16

            R = ^17∙17∙16/₄₈₀ = ²⁸⁹/₃₀ ≈ 9,6 cm

d) Finn vinklarna på triangeln.

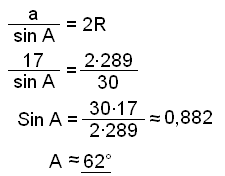
Därför är  B ≈ 62° og C ≈ 180 − 2∙62 ≈ 56°.

En median i en triangel är en sträcka ritad från en vinkel till mittpunkten på motsatt sida. Medianerna i en triangel genomskär alla varandra i en punkt. Denna punkt delar varje median i förhållandet 1: 2.

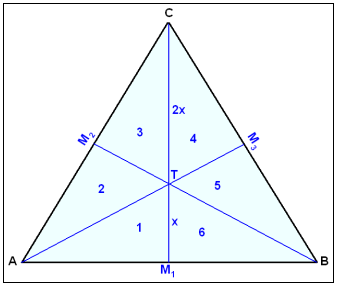
I diagrammet ovan är M₁, M₂ and M₃ mittpunkterna på triangelns sidor. Medianerna genomskär varandra i punkten T vilken delar M₁C I delarna x och 2x.

Medianerna delar triangeln i sex mindre trianglar, numrerade 1-6 i diagrammet. Dessa trianglar har alla samma area. Punkten T är därför gravitationscentrum i triangeln. Om triangeln var gjord utav material och blev utskuren så skulle vi kunna balansera den på nål eller spik placerad i punkten T.

I en liksidig triangel är centrerna på den inskrivna och omskrivna cirkeln i samma punkt.

Medianerna i en triangel genomskär varandra i en punkt.

Höjderna i en triangel genomskär också varandra i en punkt.

Exempel 4

Längden på medianen av en triangel är 24 cm. Beräkna längden på  sträckorna som de andra medianerna delar in den i.

Vi kallar en sträcka x, den andra är då 2x.

    x + 2x = 24

          3x = 24

            x = 8

Medianen är delad i sträckor utav längderna 8 cm och 16 cm

Exempel 5

En triangel ABC ritas i ett koordinationssystem.
A = (−4, −4), B = (12, 0) och C = (4, 16). Finn koordinaterna till punkten där medianerna genomskär varandra.

Vi börjar med att hitta mittpunkten på sidan BC

Nu ska vi hitta ekvationen till medianen genom A. Detta är linjen genom A  = (−4, −4) och (8, 8).

   Gradienten  k = (8 + 4)/(8 + 4) = 1

Genom att använda ekvationen för en rak linje i formen:

   y = k(x − x₁) + y₁

får vi  y = 1(x − 8) + 8

   y = x

Sedan gör vi samma sak för medianen genom punkten B. Först hittar vi mittpunkten till AC.

Ekvationen utav medianen genom B har ni hittats. Detta är linjen genom B= (12, 0) och (0, 6).

Gradienten k = (0 − 6)/(12 − 6) = −½

Därför är   y = −½(x − 0) + 6

   y = −½x + 6

Genom att lösa de två ekvationerna y = x and y = −½x + 6 får vi:

   x = −½x + 6

   x + ½x = 6

       1½x = 6

            x = 4 och därför är y = 4 också.

Medianerna genomskär varandra i punkten (4, 4).

Ceva’s Regel:

Detta är en regel som fått sitt namn efter den italienske matematikern Giovanni Ceva.

Om vi drar vilka som helst tre linjer som alla går igenom   en punkt, säg P och en vinkel på triangeln. Kalla punkterna där  de genomskär sidorna AB, AC och BC , X, Y och Z  respektive.

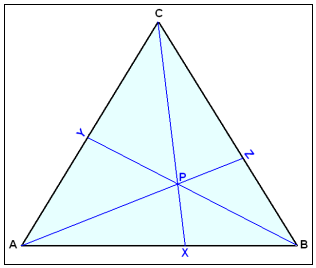
Då är regeln som följer:

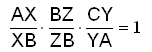
Denna regel gäller så klart för medianer, höjder och vilka som helst andra linjer som går från en vinkel av en triangel till den motsatta sidan och genomskär i en punkt.

Exempel 6

I diagrammet nedan finn längderna på sträckorna som Z delar upp BC i.

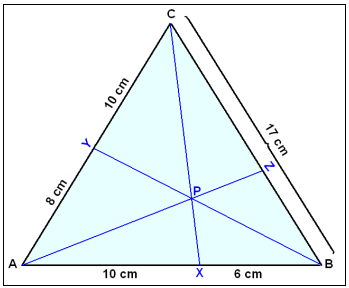
Om x = BZ, då är ZC = 17 − x. Genom att använda regeln får vi:

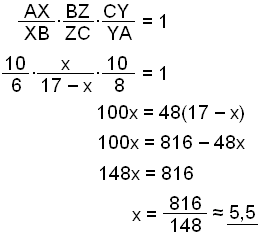
Därför delar Z upp sidan BC i sträckor med längderna 5.5 cm och 11.5 cm.

Prova Test 2 på Trianglar.  Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.