© 2008  Rasmus ehf    og Jóhann Ísak

Trigonometri Formler

Lektion 2

Formlerna för sinus, cosinus och tangenter av summan eller skillnaden av två vinklar kan vara väldigt användbar. Ett bevis på vissa av reglerna ges här

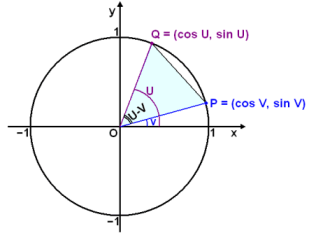
Triangeln OPQ i diagrammet har hörnorna P,, Q och O i centret av koordinatsystemet. Vi kommer kalla vinkeln mellan x-axeln och OQ för u, och vinkeln mellan x-axeln och   OP för v. Vinkeln POQ är därför u – v. Punkten Q har koordinaterna (cos u, sin u) och punkten P har koordinaterna (cos v, sin v). Avståndet mellan P och Q kan skrivas |PQ|. Nu använder vi formeln för avstånd mellan två punkter för att hitta detta avstånd.

   |PQ|2 = (cos u − cos v)2 + (sin u − sin v)2  

            = cos2u − 2 cos u cos v + cos2v

               + sin2u − 2 sin u sin v + sin2v  

            = 1 − 2 cos u cos v− 2 sin u sin v + 1

            = 2 − 2 cos u cos v − 2 sin u sin v

(avstånd)2 = (x2−x1)2 + (y2−y1)2

Multiplicera utanför parenteserna och förenkla.  

Nu finner vi |PQ| genom att använda cosinusfunktionen.

   |PQ|2 = 12 + 12 − 2∙1∙1∙cos (u − v)

             = 2 − 2∙cos (u − v)

Genom att beräkna dessa uttryck får vi:

   2 − 2∙cos (u − v) = 2 − 2 cos u cos v − 2 sin u sin v

     − 2∙cos (u − v) = − 2 cos u cos v − 2 sin u sin v

Om vi dividerar allt med −2 får vi följande formel:

cos (u − v) = cos u cos v + sin u sin v

Vi får en andra formel från denna genom att sätt in −v i formeln istället för v:

   cos (u − (−v)) = cos u cos (−v) + sin u sin (−v)

Genom att använda reglerna vi fann genom enhetscirkeln, cos (−v) = cos v and sin (−v) = − sin v kan vi skriva om detta uttryck som:

cos (u + v) = cos u cos v − sin u sin v

 

I diagrammet nedan har vi ritat två trianglar. En  har en vinkel v mellan hypotenusan och x-axeln, den andra har samma vinkel mellan hypotenusan och y-axeln. Detta betyder att de två trianglarna är kongruenta (exakt lika).

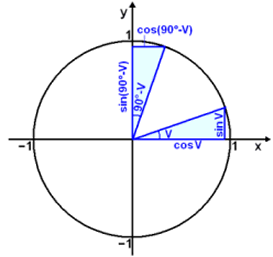
Dessa kongruenta trianglar leder till följande regler:

   cos v  = sin (90° − v)    og   sin v = cos (90° − v)

Nu ersätter vi 90° istället för u och (u + v) istället för v i dessa regler för att få två formler för sinus.

    sin (u + v) = cos (90° − (u + v))

                     = cos ((90° − u) − v)

                     = cos (90° − u) cos v + sin (90° − u) sin v

                     = sin u cos v + cos u sin v

På detta sätt har vi funnit en formel för sin (u + v):

sin (u+v) = sin u cos v + cos u sin v

Om vi nu byter ut (−v) med v i denna formel, så får vi följande:
 

sin (u − v) = sin (u + (−v))

                    = sin u cos (−v) + cos u sin (−v)

                    = sin u cos v − cos u sin v

 Vi använder regeln

cos(u−v) = cos u cos v−sin u sinv

och sedan sin v = cos (90° − v) och cos v  = sin (90° − v).

På detta sätt har vi funnit en formel för sin (u − v):

sin (u-v) = sin u cos v - cos u sin v

Genom att byta ut v med u i formlerna sin (u + v) och cos (u + v) så får vi  formler för sin (u + u) och cos (u + u), vilka kallas formlerna för dubbla vinkeln. Dessa kan skrivas som:

sin 2u = 2 sin u cos u

cos 2u = cos2 u − sin2

Regeln för cos 2u kan skrivas på ytterligare två sätt genom att använda regeln cos 2 u + sin 2 u = 1. 

Först ersätter vi cos 2 u genom att använda cos 2 u = 1 − sin 2 u och sedan sin 2 u genom att använda sin 2 u = 1 − cos 2 u, vilket ger formlerna:
 

cos 2u = 2 cos2 u − 1

cos 2u = 1 − 2 sin2 u

Exempel 1

Använd formlerna ovan för att finna exakta värden för sin 15°
och cos 15°

Vi har redan funnit att cos  45° = 2/2, sin 45° =  2/2, cos 60° = ½ och sin 60° = 3/2. Genom att använda formeln för
cos (u - v) får vi följande:

   cos 15° = cos (60° − 45°)

                 = cos 60° cos 45° + sin 60° sin 45°

                 = ½∙2/2 + 3/2∙2/2

                 = 2/4 + 3∙2/4

                 = 2∙(1 + 3)/4

Genom att använda formeln för sin (u - v) får vi följande:

     sin 15° = sin (60° − 45°)

                 = sin 60° cos 45° − cos 60° sin 45°

                 = 3/2∙2/2 − ½∙2/2

                 = 3∙2/4 − 2/4

                 = 2∙(3 − 1)/4

Exempel 2

Förenkla uttrycket sin (270° − v).

Vi använder regeln sin (u − v) = sin u × cos v − cos u × sin v.

sin (270° − v) = sin 270° cos v − cos 270° sin v

                       = −1∙ cos v − 0∙ sin v         

                       = − cos v

sin 270° = −1

 cos 270° = 0

Exempel 3

Finn en formel för cos 3x som endast använder sin x och cos x.

Vi använder formeln cos (u + v) = cos u × cos v − sin u × sin v och ersätter u
med 2x och  v med  x.

cos (2x + x) = cos 2x cos x − sin 2x sin x

cos 2x = cos2x − sin2x       sin 2x = 2 sin x cos x

                      = (cos2 x − sin2 x)∙cos x − (2 sin x cos x)∙sin x

                      = cos3 x − sin2 x cos x − 2 sin2 x cos x

                      = cos3 x − 3 sin2 x cos x

Exempel 4

Lös ekvationen sin 2x + 2 sin x = 0 på intervallet 0 x < 2.

              sin 2x + 2 sin x = 0

   2 sin x cos  x + 2 sin x = 0

         2 sin x (cos  x + 1) = 0

Använd sin 2x = 2 sin x cos x

En lösning är  sin x = 0

         x = 0 eða (0° eða 180°)

En annan lösning är  cos x = −1

          x = (180°)

Lösningarna är därför 0, and .   

Exempel 5

Lös ekvationen  7 cos2 x + 5 sin2 x + 6 sin 2x = 0

Först använder vi formeln  sin 2x = 2 sin x cos x.

   7 cos2 x + 5 sin2 x + 12 sin x cos x = 0

En ekvation av denna sort, med två faktorer av sin eller cos i varje term kan lösas genom att dividera med cos2x och ändra ekvationen till en tangentekvation.

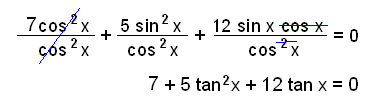
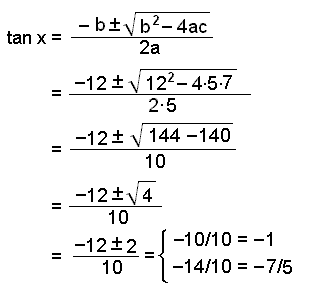
Detta är en andragradsekvation med a = 5, b = 12 och c = 7.

   tan x = −1 ger x = −/4 + k∙  (−45° + k∙180°)

   tan x = −7/5 ger inte en vinkel som är i exakt proportion till  p

         x ≈ −0,95 + k∙  (54,5° + k∙180°)

Prova Test 2 på Trigonometri Formler.

 Kom ihåg att använda checklistan för att hålla ordning på ditt arbete.