© 2009  Rasmus ehf    och Jóhann Ísak

Vektorer

Introduktion 2  

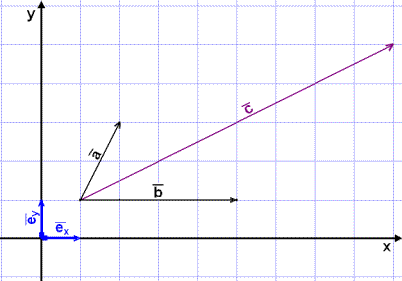
Vektorns komposanter

När vektorn är uppdelad i två andra vektorer och så att  + = säger vi att vektorn   är uppdelad i dess komposanter (se bild här nedanför).

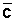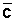Vektorer delas ofta upp i vågräta och lodräta vektorer som vi ser här ovanför eftersom dessa komponenter är viktiga i t.ex. kraftuträkningar i fysik. Generellt kan man dela upp vektorn så att dess komposanter är parallella med vilka vektorer som helst. Låt oss titta på ett bekant exempel (se bild här nedanför). Vi vill skriva vektorn med hjälp av vektorerna och , med andra ord dela upp vektorn i komposanter som är parallella med vektorerna och .

Lägg till en andra vektor till den som redan finns och sedan en och en halv vektor .

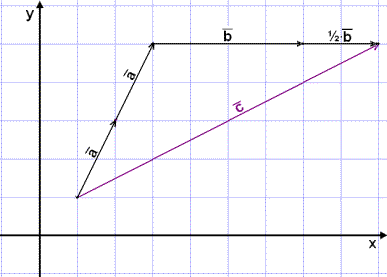
Nu ser vi att komposanterna är 2 och 1½. Vi kan dela upp alla vektorer i komposanter som är parallella med två vektorer och som inte är parallella med varandra och ingen av vektorerna är en nollvektor (har längden 0). Vi behöver bara hitta två tal t och r så att följande ekvation är giltig:

   = r∙+ t∙

Tricket är att hitta talen t och r (även kallade komponenter) så att ekvationen ovan håller.

Exempel 1

Nu ska vi dela upp vektorerna , och från bilden här ovanför i lodräta och vågräta komposanter. Vi använder en vågrät vektor som har längden 1 (en ruta) och en lika lång lodrät vektor. Dessa vektorer kallas enhetsvektorer och betecknas med
och .

Vi börjar med att dela upp vektorn .

Vi kan tydligt se på bilden att = + 2.

Som vi ser så är det lätt att räkna ut komponenterna för de två andra vektorerna. Vektorn är 4 rutor lång till höger och 0 rutor lång uppåt. Vektorn är åtta rutor lång till höger och fyra uppåt.

= 4 och = 8 + 4.

Exempel 2

En kraft på 200 N är riktad uppåt med 25° i förhållande till planet. Vad blir kraftens effekt i planets riktning och rakt uppåt?

Vi ritar upp en bild för att bättre kunna se problemet.

Nu kan vi använda trigonometriska regler för att räkna ut || och ||

En vågrät komposant som den vi räknade ut här ovanför (komposanten ) kallas för projektionen av vektorn på x-axeln. Likaså kallar man komposanten för projektionen av vektorn   på y-axeln. På bilden här nedanför kan vi se hur dessa projektioner ser ut.

Vi har nu en formel för att hitta projektionen av en vektor på x-axeln eller en vågrät vektor. Formeln är som följer:

Exempel 3

Vektorn har längden 3 och riktning 20° från planet, vektorn har längden 4 och riktning 40° från planet och vektorn har längden 5 och riktning 70° från planet. Dessa riktningar ger oss vinkeln mellan och som är 20° och vinkeln mellan och är 30°. Låt oss dela upp vektorn i komposanter som är parallella med och , men först ritar vi upp de tre vektorerna. Som vi nu ser så verkar det inte vara så lätt att hitta komposanterna, men om vi ritar in komposanterna så klarnar det en aning.

Vi måste nu hitta vektorerna r∙ och t∙ som tillsammans bildar vektorn . När vi ritar in dem sammanlagda vektorerna så får vi en triangel (blå på bilden) som har vinkeln 30° (mellan vektorerna och ) och vinkeln 20° (mellan vektorerna  och ) så, den tredje vinkeln måste vara 180°− 30°− 20° = 130°. Med andra ord, vi känner till alla vinklarna i triangeln och en sida som har längden 4 (||= 4). Det ger oss möjligheten till att använda sinussatsen.

Här använder vi sinussatsen och multiplicerar båda leden med sin 30°.

På samma sätt hittar vi t∙||

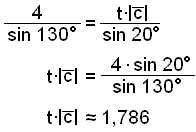
Nu har vi hittat längderna på triangelns sidor. Nu måste vi hitta talen r och t. Börja med r.

   r∙|| ≈ 2,611

      r∙3 ≈ 2,611

         r ≈ 2,611/3 ≈ 0,87

Räkna sedan ut t.

    t∙|| ≈ 1,786

      t∙5 ≈ 1,786

         t ≈ 1,786/5 ≈ 0,36

Komposanterna och deras komponenter är som följer:

   ≈ 0,87∙ + 0,36∙

Från exemplet här ovanför (Exempel 3) ser vi att vi kan använda sinussatsen för att dela upp en vektor i komposanter som är parallella med två andra vektorer. Det enda vi behöver är de 3 vektorernas riktning samt längden på den vektor som vi vill dela upp. Eftersom denna metod är så pass användbar så ramar vi in den.

När vi arbetar med vektorer i ett koordinatsystem så blir vektoruppdelning mycket enklare. I Exempel 1 introducerade vi en vågrät och en lodrät vektor, och . Dessa vektorers längd är en enhet i koordinatsystemet och kallas för enhetsvektorer.

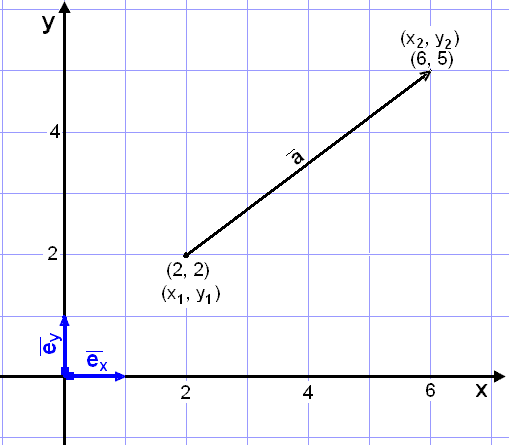
Vi kan dela upp vektorn på bilden här ovanför på samma sätt som vi gjorde i Exempel 1. Resultatet är som följer:

   = 4 + 3

För att komma från begynnelsepunkten (2, 2) till ändpunkten (6, 5) måste vi flytta oss fyra rutor (4) till höger och tre (3) upp. Vi ser att detta ger oss automatiskt att projektionen av   på x-axeln är 4 och projektionen på y-axeln är 3. Som vi ser så är det enkelt att räkna ut projektionerna i ett koordinatsystem. Vi kan även räkna ut projektionerna genom att hitta differensen mellan koordinaterna i änd- och begynnelsepunkten.

   6 − 2 = 4 och 5 − 2 = 3

Som vi vet så kan vi placera en vektor var som helst i ett koordinatsystem. Det är därför behändigt att placera vektorn i origo, (0, 0). Då blir vektorns ändpunkt (4, 3) och vi kan säga att vektorn har koordinaterna

    = (4, 3)

Denna representation av vektorn är ett enklare och rättare sätt att beskriva en vektor, för vektorn är trots allt oberoende av sin position i ett koordinatsystem. Vektorn (4, 3) beskriver en vektor som har en riktning på 4 enheter vågrätt och 3 enheter lodrätt.

Problemet med ovanstående skrivsätt är att det kan skapa en viss oklarhet med vilka koordinater man menar, vektor- eller punktkoordinater. Även om vissa böcker använder detta skrivsätt så är det vanligare att skriva vektorns koordinater på följande sätt:

Ekvationen för en vektors koordinater är som följer:

Exempel 4

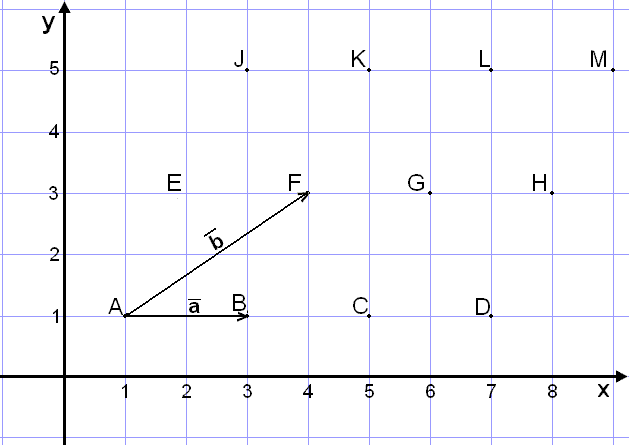
a)   Nu ska vi räkna ut koordinaterna för vektorn =

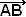
   Här har vi endast en förflyttning på två rutor till höger, det är allt. Ingen förflyttning upp eller ner så y-koordinaten måste vara 0.

   Vi kan även använda ekvationen ändpunkt (B) − begynnelsepunkt (A).

   Vi har A = (1, 1) och B = (1, 3).

b)   Nu ska vi hitta koordinaterna för vektorn =

       Vi har A = (1, 1) och F = (4, 3).

c)   Hur räknar vi koordinaterna för vektorn + ? Vi ser att om vi kopplar ihop vektorerna och så hamnar vi i punkten G och har då förflyttat oss 5 rutor till höger och 2 upp. Men vi kan även räkna ut koordinaterna på följande sätt:

d)  Låt oss nu titta på koordinaterna för vektorn - . Om vi vänder på vektorn och kopplar den till så
     får vi vektorn och den förflyttar oss en ruta till vänster och två nedåt. Men vi kan även räkna ut
     resultatet med koordinaterna.

e)   Till sist ska vi räkna ut koordinaterna för vektorn + 2. Om vi dubblar vektorn och kopplar ihop den med så hamnar vi i punkten M. Då har vi förflyttat oss 8 rutor till höger och fyra upp. Med koordinaterna räknar vi ut det samma såhär:

Slutsatsen som vi kan dra från ovanstående exempel är att vi kan använda följande regler när vi adderar  
    och subtraherar vektorer eller multiplicerar en vektor med en konstant, om de är skrivna som koordinater.

Om vi har givet vektorerna och på almänn form:

och

Då gäller följande regler:

Exempel 5

Nu ska vi lösa ett problem som är liknande det som vi hade i Exempel 3 men nu använder vi ett koordinatsystem och behöver inte använda trigonometri.

Vi har givet vektorerna , och med koordinaterna (se bild):

  och

Vi ska nu dela upp vektorn i komposanter parallella med vektorerna och så att följande ekvation  håller:   

= r∙ + t∙

Vi räknar med koordinaterna:

Det ger oss två ekvationer med två okända variabler.

   x-koordinaterna ger ekvationen 3r + 3t = 3 eller r + t = 1 och

   y-koordinaterna ger ekvationen 2r + 6t = 4 eller r + 3t = 2

Vi kan lösa ekvationssystemet genom att subtrahera x-ekvationen från y-ekvationen.

     r + 3t = 2

     −r − t = −1

           2t = 1

             t = ½  och  r = ½

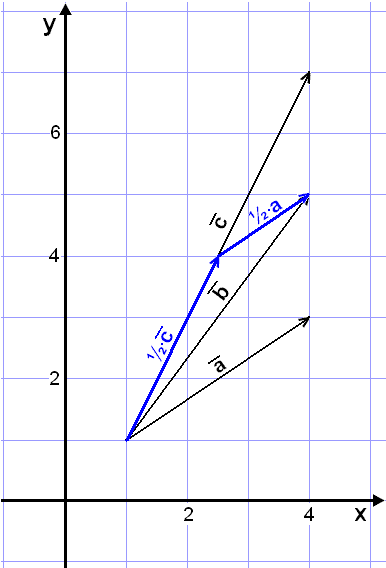
Uppdelningen blir då = ½∙ + ½∙  precis som bilden här nedanför visar.

Öva på dessa exempel och gör sedan test 2 i vektorer.

Obs! Kom ihåg att fylla i din checklista under tiden.