© 2010 Rasmus ehf och Jóhann Ísak
|
© 2010 Rasmus ehf och Jóhann Ísak |
Derivator |
|
Förändringshastighet och tangentens och sekantens k-värde
Vi introducerar nu två nya linjer.
En linje som skär åtminstone 2 punkter i en kurva kallas sekant.
En linje som har en punkt gemensam med en kurva så att både kurvan och linjen har samma riktning i den punkten kallas tangent.
Se de båda linjerna på bilden här nedanför.

Låt oss nu titta närmare på begreppen förändringshastiget och ändringskvot (genomsnittlig förändringshastighet). Förändringshastighet är ett mått på hur snabbt något förändras vid en viss tidpunkt. Ändringskvot är ett mått på hur något förändras inom ett bestämt tidsintervall, dvs. en genomsnittlig förändring.
Vi häller vatten i en stor kastrull och värmer sedan på kastrullen. Vattnets temperatur när det hälls i kastrullen är 20°C och vi mäter temperaturen varje minut under uppvärmningen. Temperaturen stiger precis som tabellen här nedanför beskriver.
| Tid(min) | Temperatur |
| 0 | 20°C |
| 1 | 30°C |
| 2 | 40°C |
| 3 | 49°C |
| 4 | 58°C |
| 5 | 66°C |
| 6 | 74°C |
| 7 | 81°C |
| 8 | 88°C |
| 9 | 95°C |
| 10 | 100°C |
Hur fort stiger temperaturen på vattnet i kastrullen?
Detta problem kan lösas på många olika sätt. Vi kan till exempel räkna ut temperaturens ändringskvot med avseende på hur lång tid det tog innan vattnet började koka (100°C).
Temperaturen steg 80 grader på 10 min.
Temperaturen steg med andra ord med 80/10 = 8°C/min i genomsnitt.
Denna metod ger oss en ganska bra idé om hur fort temperaturen steg. Om vi tittar närmare på tabellens värden så ser vi att temperaturen stiger långsammare allteftersom temperaturen blir högre. Därför är det noggrannare att räkna ut till exempel ändringskvoten för de två första och de två sista minuterna.
Ändringskvot
Första två min. = (40 – 20)/(2 – 0) = 20/2 = 10°C/min.
Sista två min. = (100 – 88)/(10 – 8) = 12/2 = 6°C/min.
Exempel 2
Vi tänker oss att funktionen f(x) = ¼x2 representerar någon form av tillväxt precis som i exempel 1 här ovanför där x är antalet minuter. Vi tittar närmare på denna tillväxt och ställer upp en värdestabell.
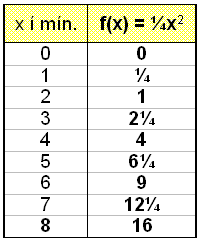
Ändringskvoten
för hela tidsintervallet är (16 – 0)/8 = 2
för de två första minuterna är (1 – 0)/2 = ½
för de sista två minuterna är (16 – 9)/(8 – 6) = 7/2 = 3½
Vi kan även räkna ut ändringskvoten för ett intervall, till exempel mellan 3 till och med 5 minuter.
Ändringskvoten för intervallet 3. – 5. min = (6¼ – 2¼)/(5 – 3) = 2
Vi ser att formeln för ändringskvoten mellan x1 min. till och med x2 blir som följer:
|
Ändringskvot
= |
Om vi använder y istället för f(x), vilket i princip är samma värde, så kan vi skriva om formeln för ändringskvoten såhär:
|
Ändringskvot
= |
Detta är formeln för lutning på en linje som går igenom de två punkter som används i formeln. Med andra ord är ändringskvoten lika med lutningen på den sekant som skär de två punkterna.
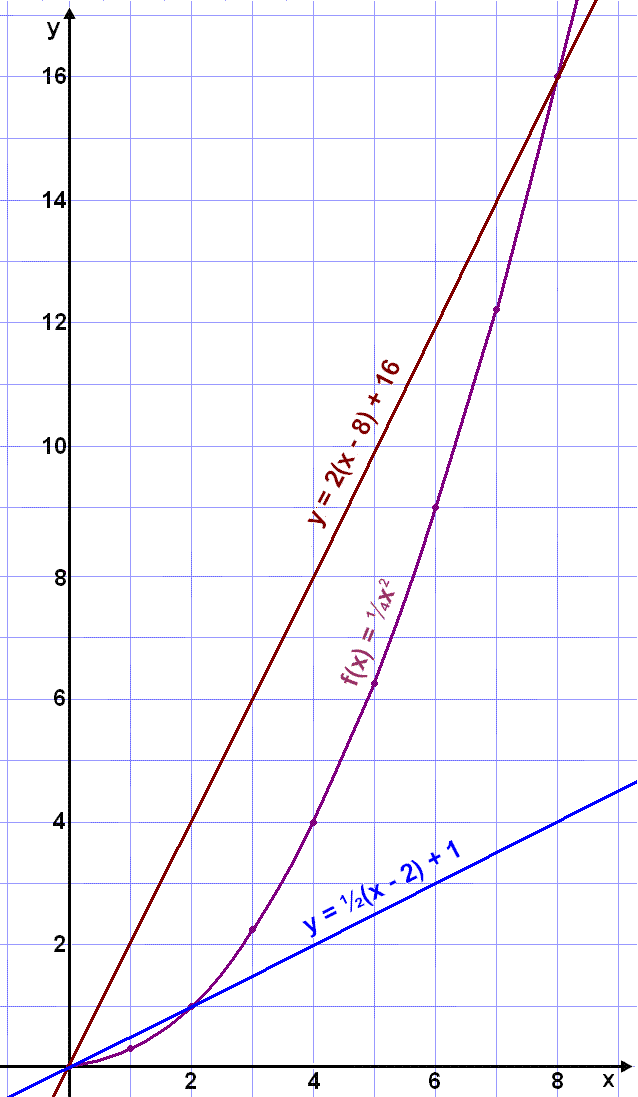
Grafen här nedanför visar två möjliga sekanter, en som visar lutningen för hela tidsintervallet och en annan som visar lutningen för de första två minuterna. Sekanternas ekvationer hittar vi genom att sätta lutningen (k-värdet) lika med ändringskvoten och punkterna får vi ut ur tabellen. Sedan sätter vi in informationen i räta linjens ekvation y = k(x – x1) + y1.
|
Ändringskvoten för intervallet x1 ≤ x ≤ x2 är
|
Räkna ut ändringskvoten för f(x) = x3 i intervallet –2 ≤ x ≤ 2.
Först räknar vi ut våra punkter.
x1 = –2 och f(–2) = (–2)3 = –8
x2 = 2 och f(2) = 23 = 8
Ändringskvoten är
![]()
Vi tar ytterligare en titt på funktionen f(x) = ¼x2. Räkna ut ändringskvoten i närheten av x = 4. Börja från vänster och minska avståndet från 4 i några steg (se värdetabellen i exempel 2).
Ändringskvoten för intervallet 1 ≤ x ≤ 4 är (4 – ¼)/(4 – 1) = 1¼
Ändringskvoten för intervallet 2 ≤ x ≤ 4 är (4 – 1)/(4 – 2) = 1½
Ändringskvoten för intervallet 3 ≤ x ≤ 4 är (4 – 2¼)/(4 – 3) = 1¾
Bilden här nedanför visar de sekanter som motsvarar våra uträkningar.
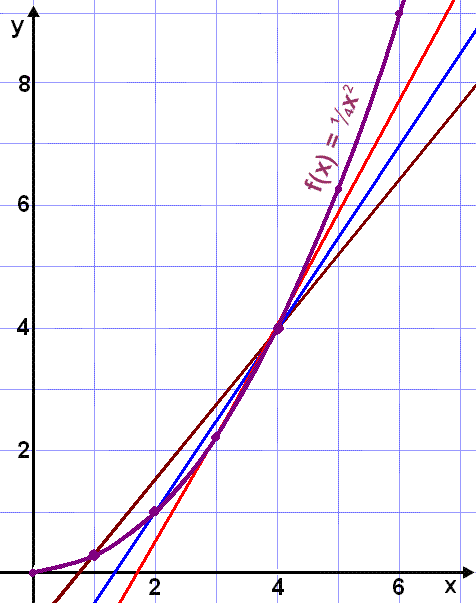
Vi har nu ett "knippe" av sekanter som lutar mer och mer allt eftersom vi minskar avståndet. Men nu ska vi förflytta oss från höger sida.
Ändringskvoten för intervallet 4 ≤ x ≤ 7 är ( 12¼ – 4)/(7 – 4) = 2¾
Ändringskvoten för intervallet 4 ≤ x ≤ 6 är (9 – 4)/(6 – 4) = 2½
Ändringskvoten för intervallet 4 ≤ x ≤ 6 är (6¼ – 4)/(6 – 5) = 2¼
Utifrån våra uträkningar så ser vi att ändringskvoten i närheten av x = 4 är i intervallet 1¾ till 2¼.
Nu ska vi räkna ut vad ändringskvoten blir för funktionen f(x) = ¼x2 i ett litet intervall runt x = 4. Vi väljer en punkt som är något större än x = 4, till exempel punkten 4 + h där h är ett litet tal nära noll. Då kan vi räkna ut ändringskvoten för ett intervall med längden h.
Vi tänker oss att bilden här nedanför visar en förstoring av grafen för funktionen f(x) = ¼x2 i närheten av punkten (4, 4). En sekant är inritad som går igenom punkterna (4, 4) och (4+h, f(4+h)).
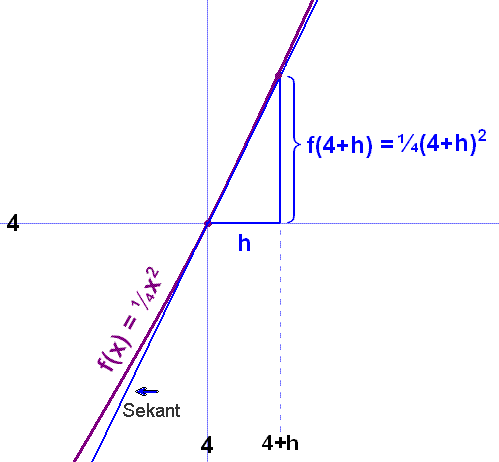
Nu är f(4+h) = ¼(4 + h)2 = ¼(16 + 8h + h2) = 4 + 2h + ¼ h2.
Sekanten skär därför punkterna (4, 4) och (4+h, 4+2h+¼h2) och ändringskvoten blir
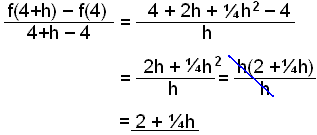
Nu kan vi välja ett litet h, t.ex. h = 0,04.
Det ger ändringskvoten 2 + ¼·0,04 = 2,01.
Och så kan vi välja ett ännu mindre h, t.ex. h = 0,0004.
Det ger ändringskvoten 2 + ¼·0,0004 = 2,0001.
på så vis kan vi låta intervallet minska till önskad storlek och vi ser att när intervallet minskar så närmar sig ändringskvoten 2
men sen är just ![]()
Detta gränsvärde ger oss förändringshastigheten i punkten (4, 4). En linje som är ritad på samma sätt som sekanten här ovan på bilden skär då endast en punkt och är då en tangent med lutning motsvarande förändringshastigheten i punkten (4, 4).
Om vi sätter in resultatet i en ekvation på enpunktsform för en linje så får vi ut tangentens ekvation i punkten.
y = 2(x – 4) + 4 = 2x – 8 + 4 = 2x – 4
y = 2x – 4
|
En tangents lutning i punkten (a, b) är
En tangents ekvation i punkten (a, b) är y = k(x – a) + b |
Först räknar vi ut lutningen.
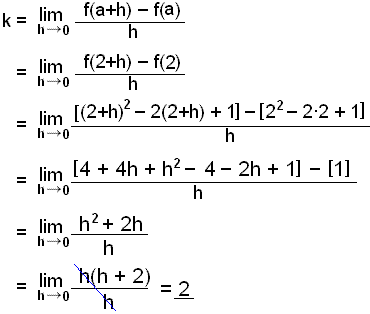 |
Hakparenteserna grupperar
|
Tangentens ekvation blir då
y = 2(x – 2) + 1
= 2x – 4 + 1
y = 2x – 3
Låt oss titta på resultatet i en graf på en CASIO grafräknare.
 |
 |
Sätt in funktionerna.

Så här ser grafen ut:
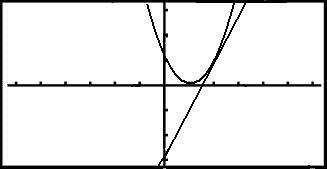
Kurvan och tangenten möts i punkten (2, 1) så tangentens ekvation måste vara rätt.
Vi kan även låta grafräknaren räkna ut lutningen på tangenten.
Vi väljer RUN och sedan knappen som det står OPTN på, som är bredvid SHIFT-knappen.
|
|
 |
|
 |
||
Därefter väljer vi CALC med F4 och d/dx med F2, där d/dx betyder ändringskvot över ett mycket litet intervall (i vissa böcker skrivs det som dy/dx). Sedan skriver vi in funktionen och x-koordinaten för punkten som vi vill veta lutningen i och detta skrivs isär med ett kommatecken precis så som bilden visar.
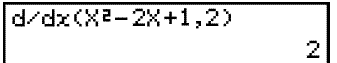
Resultat blir 2 precis som väntat.
Öva på dessa exempel och gör sedan test 1 i derivator.
Obs! Kom ihåg att fylla i din checklista under tiden.