© 2010 Rasmus ehf och Jóhann Ísak
|
© 2010 Rasmus ehf och Jóhann Ísak |
Derivator |
|
Derivera polynom
En tangents lutning varierar beroende på vilken punkt vi väljer på en kurva. En kurva bildas av ett matematiskt sammanhang eller en formel (som vi oftast kallar f(x)). Därför måste även tangentens lutning bero på ett matematiskt sammanhang eller en formel om funktionen är sammanhängande.
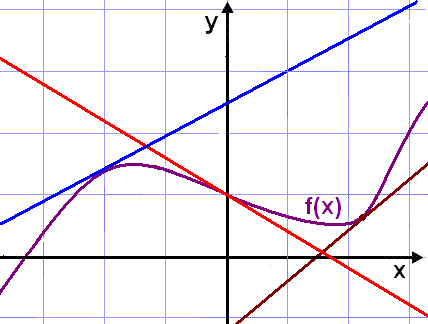
På bilden här ovanför ser vi tre inritade tangenter i olika färger. Lägg märke till att den röda linjen skär kurvan f(x) i punkten (0,1). Lutningen är lika med ändringskvoten för ett mycket litet intervall runt punkten (0, 1) precis som för de två andra tangenterna. Tangenterna har uppenbarligen olika lutning beroende på vilken punkt på kurvan f(x) de tangerar. Låt oss nu utforska möjligheten att det finns en almänn formel eller en funktion av x som ger oss lutningen för vilken punkt som helst på en kurva. Sådana funktioner kallas för derivator och skrivs vanligtvis med en apostrof. På så vis är en funktion som ger en tangents lutning för kurvan f(x) med avseende på olika x skriven som f´(x) eller y´ (även skrivsättet dy/dx används).
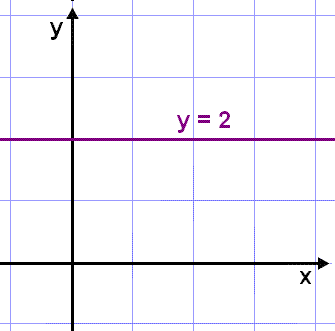
Låt oss först titta på en konstant funktion, t.ex. f(x) = k där k är en konstant. Vi använder som exempel funktionen f(x) = 2. Bilden Här nedanför till vänster visar grafen.
 |
 |
Tangenten till en linje måste vara den samma som linjen eftersom hela linjen har samma lutning i alla punkter. Derivatan för en konstant funktion är därför dess lutning. Lutningen på en vågrät linje är 0 så vi kan säga att om f(x) = 2 då är f´(x) = 0. Detta gäller för alla konstanta funktioner så att om f(x) = k då är f´(x) = 0.
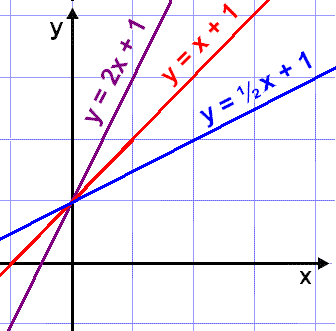
På bilden ser vi tre linjer med olika lutning. Linjernas derivator är som följer:
y = 2x + 1 har derivatan y´
= 2
y = x + 1 har derivatan y´ = 1
y = ½x + 1 har derivatan y´ = ½
linjära ekvationer på formen f(x) = ax + b har derivatan f´(x) = a.
Härnäst tittar vi på funktionen f(x) = x2.
Vi ska försöka lösa gränsvärdet ![]() utan att använda en specifik punkt.
utan att använda en specifik punkt.
|
För derivator gäller följande almänna definition:
|
Vi löser gränsvärdet för f(x) = x2.
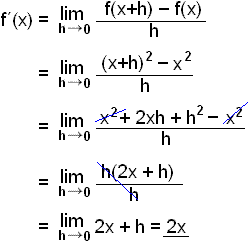 |
När vi räknar ut f(x+h) så använder vi (x+h) i stället för x i funktionen |
Derivera funktionen f(x) = 2x2 + 4x.
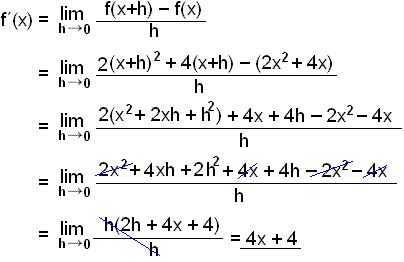
Lägg märke till att 2·x2
har derivatan 2·2x och vi kan läsa ut att derivatan av x2 är 2x. linjen y = 4x har k-värdet(lutningen) 4 så
4x har derivatan 4. När vi deriverat de båda delarna av funktionen lägger vi ihop dem och ser att derivatan av
2x2 + 4x blir
4x + 4. Vi ställer upp följande regel:
|
f(x) = ax2 + bx + c har derivatan f´(x) = 2ax + b. |
Derivera funktionen ![]() .
.
Vi har sett att när en funktion är multiplicerad med ett tal så blir derivatan multiplicerad med samma tal. Nämnaren i ett bråk fungerar på samma sätt. Vi multiplicerar täljarens alla led med bråket, i detta fall ½. När nämnaren är en konstant (dvs ett fast tal) så kan vi låta den vara. Kom ihåg att derivatan av ¼ är 0 precis som vilken annan konstant som helst.
![]()
Detta bråk kan vi förkorta.
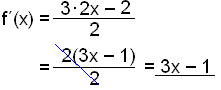
Derivera funktionen f(x) = x3.
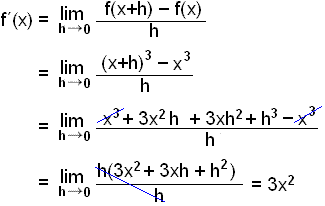
Derivera funktionen f(x) = x4.
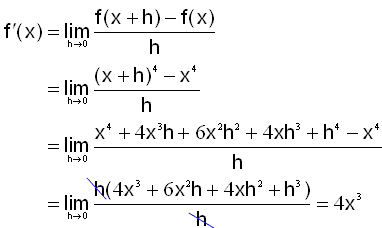
Exemplen här ovanför har visat oss en utav deriveringsreglerna.
f(x) = x0
har derivatan f´(x) = 0
f(x) = x1 har derivatan f´(x) = 1·x0
f(x) = x2 har derivatan f´(x) = 2·x1
f(x) = x3 har derivatan f´(x) = 3·x2
f(x) = x4 har derivatan f´(x) = 4·x3
Det verkar som att potensen har flyttats ner framför parametern och x blir upphöjt till potensen minus 1. Det går att bevisa att följande regel gäller:
|
f(x) = x n har derivatan f´(x) = n·x n–1 |
Derivera polynomet f(x) = x5 – 2x4 + 3x3 – 4x2 + 5x – 6.
f´(x) = 5x4
– 2·4x3 + 3·3x2
– 4·2x + 5 – 0
= 5x4 – 8x3 + 9x2 – 8x + 5
Hitta tangentens ekvation för funktionen f(x) = x5 – 5x3 + 4x i x = 1.
Vi börjar med att räkna ut y-koordinaten i tangeringspunkten.
f(1) = 1 – 5 + 4 = 0
Tangeringspunkten är (1, 0).
Derivera sedan funktionen.
f´(x) = 5x4 – 5·3x2 + 4
= 5x4 – 15x2 + 4
Derivata är en formel för lutning så nu kan vi räkna ut lutningen på tangenten som är f´(1).
f´(1) = 5 – 15 + 4 = –6
Vi använder värdena i enpunktsformen för en linje.
y = –6(x – 1) + 0
y = –6x + 6

|
Till sist ska vi titta på grafen i en grafritande räknare.
|
|
|
|
En tangents ekvation i punkten (a, f(a)) är y = f´(a)(x - a) + f(a) |
Öva på dessa exempel och gör sedan test
2 i derivator.
Obs! Kom ihåg att fylla i din checklista under tiden.