Faktorisering.
| © 2007 Rasmus ehf och Jóhann Ísak Pétursson |
Faktorisering. |
|
Lektion 5 Parenteser vilka är gemensamma faktorer
| Du vet hur man multiplicerar ihop två parenteser. | ||
|
(a + b)(c + d) = ac + ad +
bc
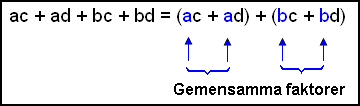
+ bd Om du har uttrycket på höger sida hur gör du då för att ändra tillbaka det till de två parenteserna på den vänstra sidan?Här följer ett systematiskt sätt att gå till väga. Först sätter du termerna inom parentes två och två och noterar att varje parentes har en gemensam faktor.
|
||
 |
||
| Ta ut denna faktor ur varje parentes | ||
|
|
= (c + d)(a + b)Nu ser du att båda parenteser är exakt likadana | |
|
Alltså är parenteserna i sig gemensamma faktorer utav uttrycket och kan därför faktoriseras bort. |
||
|
|
||
|
Om du tycker att det är svårt att förstå så tänk på parentesen som ett enskilt tal, vi kan kalla det S. Då ser uttrycket ut på följande sätt. ac + ad + bc + bd = (ac + ad) + (bc + bd) |
||
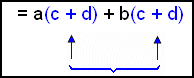 |
||
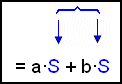 |
Kalla parentesen S och skriv S istället för parentesen. | |
| = S(a + b)= (c + d)(a + b) |
Sätt S utanför parentesen. Slutligen sätter du tillbaka parentesen istället för S. |
|
|
Lägg märke till att det inte spelar någon roll vilket par utav termer vi sätter ihop inom parentes. Om vi organiserar om termerna och sedan sätter de inom parentes så skulle exemplet se ut på följande sätt. |
||
| ac + ad + bc + bd | = (ac + bc) + (ad + bd) | |
|
= c(a + b)+ d(a + b) = (c(a + b) + d(a + b)) = (a + b)(c + d)Slutresultatet är detsamma som förut. |
||
Exempel 1
| Faktorisera x2 + x + ax + a. | |
|
x2 + x + ax + a |
= x(x + 1) + a(x + 1) |
| = (x + 1)(x + a) | |
Exempel 2
|
Faktorisera x3 − 4x2 − x + 4. |
|
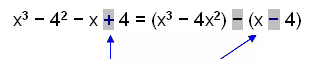 |
|
|
Notera att plustecknet ändras till ett minustecken när vi sätter in det i en parentes som har ett minustecken framför sig. Det är för att uttrycket ska förbli detsamma om vi tar bort parenteserna. |
|
|
= x2(x − 4) − (x − 4) |
= (x − 4)(x2 − 1) |
|
Vi kan faktorisera den andra parentesen igen eftersom den utgör differensen utav två kvadrater |
= (x − 4)(x + 1)(x − 1) |
Exempel3
|
Faktorisera 6x2 + 13x + 6. |
|
| 6x2 + 13x + 6 = 6x2 + 4x + 9x + 6 | |
|
Först måste vi dela 13x i två delar. För att finna dessa delar så multiplicerar vi koefficienten utav, x2., 6, med den konstanta koefficienten vilken också är 6. Det ger oss 36. Nu måste vi hitta de två talen som vid addering blir 13 och vid multiplikation blir 36. Dessa två tal är enkla att hitta, , de är 4 och 9. Vi delar upp 13x i 4x och 9x. Nu kan vi faktorisera bort en parentes. |
|
| = (6x2 + 4x) + (9x + 6) | = (2x(3x + 2) + 3(3x + 2)) |
| = (3x + 2)(2x + 3) | |
Prova test 5 på faktorisering. Om du får 80% eller högre antal rätt så går du vidare till nästa ämne.