Trigonometri (sin, cos och tan)
| © 2004 Rasmus ehf |
Trigonometri (sin, cos och tan) |
Introduction 1
Studera en rätvinklig triangel
|
|
Vinkeln A är 30 grader. Det kan skrivas
|
a betecknar motstående sida till vinkeln A.
b betecknar motstående sida till vinkeln B.
c betecknar motstående sida till vinkeln C.
Trianglar med lika stora vinklar är likformiga
|
|
I dessa trianglar är kvoten mellan två sidor i den ena triangeln lika stor som kvoten mellan motsvarande sidor i den andra. |
Exempelvis har vi att
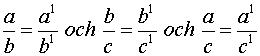
Hur stor denna kvot är beror på vinklarnas storlek.
Tangens
|
|
Tangens (tan) för spetsig vinkel i rätvinklig triangel är kvoten mellan motstående sida och närstående sida. |
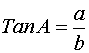
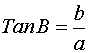
Exempel 1 Räkna vinkeln A
|
|
Först
|
För att räkna vinkeln får vi använda inversen av tangens funktionen tan-1, den finns på räknemaskinen.
Vägledning med nyare maskiner:
shift - tan-1 0,75 =37º
Använd räknemaskinen, framåt och tillbaks:
Vinkeln → kvoten kvoten → vinkeln
Tan 37º = 0,75 0,75 = Tan 37º
Exempel 2 Räkna sidan b
|
|
Tan 37º = 4/b Tan 37º · b = 4 0,7· b = 4 b=5
|
Sinus
|
|
Om <A är en spetsig vinkel i rätvinklig triangel då är Sinus av A kvoten mellan motstående sida och hypotenusan. |
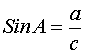
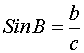
Exempel 3 Räkna sinus av A och vinkeln A i hela grader.
|
|
Sin A = 3/5 = 0,6 gör 37º Shift sin-1 0,6 = 37º |
Exempel 4 Räkna a.
|
|
Sin 37º = a/5 a = Sin 37º · 5 a = 3 |
Kosinus
|
|
Om A är en spetsig vinkel i rätvinklig triangel, då är Kosinus av A kvoten mellan närstående sida och hypotenusan. |
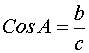
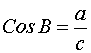
Exempel 5 Räkna kosinus av A och vinkeln A i hela grader.
|
|
Cos A = 4/5 = 0,8 gör 37º Shift cos-1 0,8 = 37º |
Exempel 6 Räkna b.
|
|
Cos 37º = b/5 b = Cos 37º · 5 b = 4 |
Några resultat för sin, cos og tan.
| Sin 80º = 0,98 | Cos 80º = 0,17 | Tan 80º = 5,67 |
| Sin 60º = 0,87 | Cos 60º = 0,5 | Tan 60º = 1,73 |
| Sin 30º = 0,5 | Cos 30º = 0,87 | Tan 30º = 0,58 |
| Sin 10º = 0,17 | Cos 10º = 0,98 | Tan 10º = 0,18 |
Öva på dessa metoder och gör
sedan test 1 trigonometri (sin, cos og tan).
Obs! Kom ihåg att fylla i din checklista under tiden.