© 2006  Rasmus ehf  og Jóhann Ísak Pétursson

Factorising.

 Print

Lesson 5   

Brackets that are common factors

You know how to multiply two brackets together.
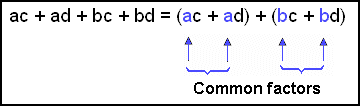
(a + b)(c + d) = ac + ad + bc + bd

If you have the expression on the right hand side how can you change it back to the two brackets on the left hand side?

Here’s a systematic way to go about it. First bracket the terms together two by two and note that each of the brackets has a common factor.

Take this factor outside each bracket.

Now you see that both of the brackets are exactly the same.

= (c + d)(a + b)

 

In other words the brackets themselves are common factors of the expression and can be factored out .                              

 

If you find this hard to understand think of the bracket as being a single value, we can call it S. Now the expression looks like this:

ac + ad + bc + bd = (ac + ad) + (bc + bd)
 
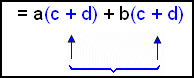    Call the bracket S and write S instead of the bracket.
= S(a + b)= (c + d)(a + b)

Take S outside the bracket.

Finally put the bracket back instead of the S.

Notice that it doesn’t matter which pair of terms we bracket together. If we rearrange the terms and then bracket them together the example would look like this:

 
ac + ad + bc + bd = (ac + bc) + (ad + bd)
 

= c(a + b)+ d(a + b)

= (c(a + b) + d(a + b))

= (a + b)(c + d)

The end result is the same as before.

Example 1                          

Factorise x2 + x + ax + a.

 x2 + x + ax + a

= x(x + 1) + a(x + 1)
  = (x + 1)(x + a)

Example 2                         

Factorise x3 − 4x2 − x + 4.

Notice that the plus sign changes to a minus when we put it in a bracket that has a minus sign in front of it. This is so that the expression stays the same if we remove the brackets again.

 = x2(x − 4) − (x − 4)

 = (x − 4)(x2 − 1)    

We can factorise the second bracket again asit is the difference of two squares.

= (x − 4)(x + 1)(x − 1)

Example 3

Factorise   6x2 + 13x + 6.
6x2 + 13x + 6 = 6x2 + 4x + 9x + 6

First we need to split the 13x into two parts. To find these we multiply the coefficient of x2 , 6, by the constant coefficient also 6. This gives 36.

Now we need to find two numbers that add up to 13  but give 36 when multiplied together. These two numbers are easy to find, they are 4 and 9.

So we split 13x up into 4x and  9x. Now we can factorise out a bracket.

= (6x2 + 4x) + (9x + 6)  = (2x(3x + 2) + 3(3x + 2))
  = (3x + 2)(2x + 3)

Try Quiz 5 on Factorising. If you score 80% or higher, go to the next topic.