© 2008  Rasmus ehf
and Jóhann Ísak

Trig functions

  Print

Lesson 4  Trig equations and inequalities

Example 1

Solve the equation 2cos 3v° = 1 on the interval 0°   v° < 360°.

   cos 3v° = ½

The calculator gives the following:

   3v° = cos−1 (½) = 60° + k∙360° 

     v° = 60°/3 + k∙360°/3        k is a whole number, positive or negative

     v° = 20° + k∙120°   

If we put k = 0, 1 og 2 we get the following solutions on the interval 0°   v° < 360°:

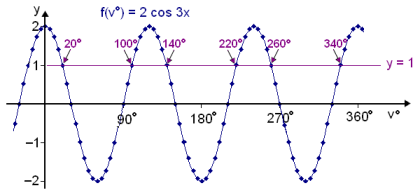
   20°, 140° and 260°

But this is only half the answer. We need to remember the rule cos x = cos (−x) that can be seen by looking at the unit circle.

This gives the following solutions:

   3v° = −60° + k∙360°

     v° = −60°/3 + k∙360°/3

     v° = −20° + k∙120°

If we put k = 1, 2 and 3 we get three more solutions:

   100°, 220° and 340°

The six solutions are therefore:

   20°, 100°, 140°, 220°, 260° and 340°

We can see these solutions graphically by drawing two graphs. First the wave f(v°) = 2∙cos 3v°, then the horizontal line  y = 1 which are the left and  the right hand side of the equation. The points of intersection of these two graphs are the solutions of the equation.

Example 2

Solve the equation sin x = ½ on the interval 0 x < 4.

If we use a calculator and want to give our answer as ratios of , we need to set the calculator to degrees and then change to radians by multiplying by /180° and cancelling as much as possible. If we are satisfied with answers as decimal fractions we can set the calculator to radians.

We’ll work with the calculator set to degrees.

   x = sin−1(½) = 30°∙ /180° = /6

   x = /6 + k∙2   (+ k∙12/6)

      = /6, 13/6 (25/6, 37/6 etc.)

Using k = 0 and
 k = 1. 2 is the same as 12/6.

This gives us two solutions on the required interval.
Now we need to find the other solutions that the calculator does not give us but that we have seen on the unit circle.
We use the rule  sin x = sin ( − x) , the calculator only gives us the solution x, not  ( − x).

   x = sin−1(½) =30°∙/180°= /6

   x = − /6 + k∙2

      = 5/6 (= 150°) + k∙2

      = 5/6, 17/6 etc.

The following solutions are on the interval 0 x < 4:

   /6, 5/6, 13/6 and 17/6

Example 3

Solve the equation 2∙sin 4(x − /4) = 1 on the interval
 0 x < 2.

   2∙sin 4(x − /4) = 1

      sin 4(x − /4) = ½

            4(x − /4) = sin−1(½) = 30° ∙/180° = /6        

                 4x − = /6 + k∙2          

                   4x = + /6 + k∙2          

                            = 7/6 + k∙2

                         x = 7/24 + k∙/2        

Move over, simplify then divide by 4.

(+ k∙12/24)

This gives the x values 7/24, 19/24, 31/24 og 43/24 for
k = 0,1, 2 and 3.

Now we need to find the solutions that the calculator doesn’t give us.

   4x − = ( − /6) + k∙2

         4x = 2 − /6 + k∙2

         4x = 11/6 + k∙2

           x = 11/24 + k∙/2           (+ k∙12/24)

This gives the x values  11/24, 23/24, 35/24 og 47/24 for k = 0, 1, 2 and 3.

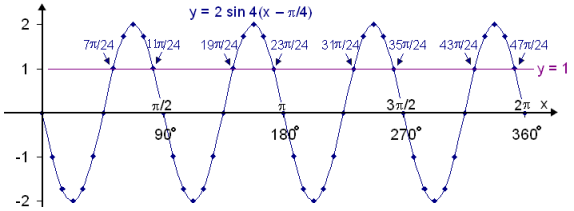
There are therefore the following eight solutions on the required interval:

7/24, 11/24, 19/24, 23/24, 31/24, 35/24, 43/24 and 47/24.

(52.5°, 82.5°, 142.5°, 172.5°, 232.5°, 262.5°, 322.5° and 352.5°.)

Draw the two graphs f(x) = 2∙sin 4(x − /4) and y = 1. The points of intersection of these two graphs give the solutions of the equation.

 

Example 4

Solve the inequality cos 2x ½ on the interval 0 <  x < 2.

First solve the equation cos 2x = ½.

   2x = cos−1(½) = 60°∙/180° = /3 + k∙2

     x = /6 + k∙

Divide through by 2.

If we choose k = 0 and 1 we get the solutions /6 and 7/6 (30° and 210°).

The calculator does not give the negative solutions.
As in a previous example we find these by using the rule
 cos x = cos (−x)):

   2x = −/3 + k∙2

     x = −/6 + k∙

Divide through by 2.

If we use the values k = 1 and 2 we get the solutions 5/6 and 11/6 (150° og 330°).

Now we draw a diagram so that we can see the solutions to the inequality.

The diagram shows the graphs of y = cos 2x and  y = ½. The shaded intervals above the horizontal line show the solutions to the inequality. The solutions are therefore the following intervals:

   0 x /6  or  5/6 x 7/6  or 11/6 x < 2

Example 5

Solve the inequality tan ½(x − /2) 1 on the interval
0 x < 2.

First we solve the equation tan ½(x − /2) = 1

   ½(x − /2) = tan−1(1) = 45°∙/180° + k∙

   ½(x − /2) = /4 + k∙  

        x − /2 = /2 + k∙2

Multiply through by  2 and move /2 over.

                 x = /2 + /2 + k∙2

                 x = + k∙2

This equation has only one solution on the interval 0 x < 2 and that is x = .

Now draw the graphs of f(x) = tan ½(x − /2) and the horizontal line y = 1.

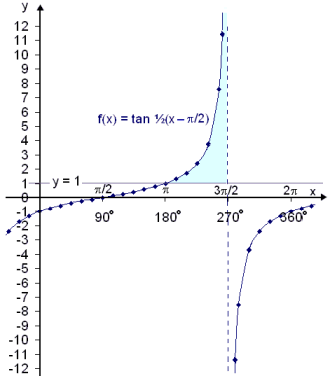
In the diagram we see that the graph of f(x) = tan ½(x − /2) is above the line y = 1 between x = and the vertical asymptote in x =  3/2 (see the shaded area in the diagram). We can’t include the asymptote in the solution as f(x) does not exist in that point. The solution of tan ½(x − /2) 1 is the interval
  x < 3/2.

Try Quiz 4 on Trig functions.
Remember to use the checklist to keep track of your work.