Functions I
| © 2007 Rasmus ehf and Jóhann Ísak |
Functions I |
Lesson 3
Second degree functions
Let’s looks again at second degree polynomials. The simplest form of the function is f(x) = x2. The graph is a parabola often called the basic parabola.

Notice that the graph is symmetrical about the y- axis. The y- axis is called the axis of symmetry of this function.
Now we will look at how the coefficients affect the appearance of the graph.
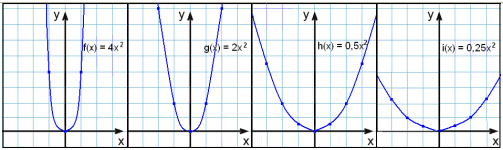
The coefficient of x2 is usual called a. If we look at parabolas with different values of a we see that some are wider and some are narrower than the basic parabola where a = 1.
Here are graphs of parabolas where a = 4, 2, ½ og ¼.
a = 4 a = 2 a = ½ a = ¼
Here are parabolas with negative values of a

a = −4 a = −2 a = −½ a = −¼
If the value of a is positive the graph bends upwards ( like a smile! ) The bigger the value of a the narrower the graph.
As a gets small the
graph becomes flatter and flatter until, when a becomes negative it turns down (
like a frown! ).
Example 1
Now we will draw the graph of f(x) = x2 + 1 and compare it with g(x) = x2.
| x | f(x) = x2 + 1 | 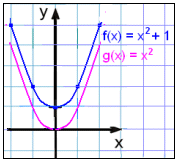 |
| -2 | (-2)2 + 1 = 5 | |
| -1 | (-1)2 + 1 = 2 | |
| 0 | 0 + 1 = 1 | |
| 1 | 12 + 1 = 2 | |
| 2 | 22 + 1 = 5 |
The values of the function ( y values ) in the table of values for f(x) = x2 +1 are all one higher than the corresponding values in the table of values for g(x) = x2 and the graph has been translated vertically by 1 unit.
Note that the grah of f(x) = x2 + 1 does not cross the x- axis. This tells us that the equation x2 + 1 = 0 has no solution. We know this already as a squared number is never negative, so x2 can never be equal to -1.
Example 2
Draw the graph of f(x) = x2 − 1 and compare it to g(x) = x2.
| x | f(x) = x2 - 1 |  |
| -2 | (-2)2 - 1 = 3 | |
| -1 | (-1)2 - 1 = 0 | |
| 0 | 0 - 1 = -1 | |
| 1 | 12 - 1 = 0 | |
| 2 | 22 - 1 = 3 |
Now the function values in the f(x) table are all one lower than the corresponding values in the table for g(x) = x2 and the graph has moved down by one unit.
Notice that in this example the graph of f(x) = x2 − 1 crosses the x – axis in two places.
This means that the equation x2 − 1 = 0 has two solutions,
x2 − 1 = 0
x2 = 1
x = ±1
which are x = −1 and x = 1.
Example 3
Draw the graph of f(x) = (x + 1)2 ( or f(x) = x2 + 2x + 1) and compare it to the basic parabola g(x) = x2.
| x | f(x) = (x+1)2 |  |
| -3 | (-3 + 1)2 = 4 | |
| -2 | (-2 + 1)2 = 1 | |
| -1 | (-1 + 1)2 = 0 | |
| 0 | (0 + 1)2 = 1 | |
| 1 | (1 + 1)2 = 4 |
Here we have added 1 to x and we can see that the function values in the table of values have all moved up by one row compared to the basic function.
The graph of f(x) is the same as the if we move the graph of g(x) = x2 one unit to the left.
We say that the basic graph has been translated by -1 units horizontally. The axis of symmetry is now x = −1.
Example 4
Draw the graph of f(x) = (x − 2)2 − 1 (or f(x) = x2 − 4x + 3) and compare it to the basic graph g(x) = x2.
If we use the same method as in the previous example we can guess that the graph has moved two units to the right and one unit down. Now we will check this by making a table of values, beginning with x = 0 and drawing the graph.
| x | f(x) = (x - 2)2 - 1 |  |
| 0 | (0 - 2)2 - 1= 3 | |
| 1 | (1 - 2)2 - 1= 0 | |
| 2 | (2 - 2)2 - 1 = -1 | |
| 3 | (3 - 2)2 - 1 = 0 | |
| 4 | (4 - 2)2 - 1 = 3 |
Notice that the axis of symmetry is now x = 2.
We can find where the graph goes over the y-axis without drawing the graph. We do this by calculating f(0) = 3 or by multiplying out the brackets and seeing that the constant term (the term without x) is 3.
f(x) = (x − 2)2 − 1 = x2 − 4x + 4 − 1 = x2 − 4x + 3 or
f(0) = (x − 2)2 − 1 = 4 − 1 = 3
Example 5
Find where the graph of f(x) = (x − 2)2 − 1 crosses the x-axis. We put y = f(x) = 0 and then solve the equation for x.
| (x − 2)2 − 1 = 0 | First move the -1 over the equal sign. |
| (x − 2)2 = 1 | Next, take the square root of both sides of the equation. Remember the + and −. |
| x − 2 = ±Ö1 = ±1 | Finally move the 2 across to the other side and simplify the result. |
| x = 2 ± 1 |
The points of intersection are x = 2 −1 = 1 and x = 2 + 1 = 3.
It is easy to see that writing the function as f(x) = (x − 2)2 − 1 gives us a lot of information.
It tells us how the basic graph is translated vertically and horizontally.
It also tells us where the axis of symmetry is.
Finally, we can easily find the points of intersection with the x and y axes.
The general form of the equation written in this way is:
f(x) = a(x + r)2 + s
a is the coefficient of x2 as we have already seen.
The axis of symmetry has the equation x = −r ( or we can say it has the same value as r but with the opposite sign).
Because of this it’s important to know how to rewrite the function
f(x) = ax2 + bx + c in the form f(x) = a(x + r)2 + s
Example 6
Now let’s look at how we can change a second degree function from one form to the other.
Rewrite f(x) = x2 − 4x + 3 in the form f(x) = (x − 2)2 − 1.
Comparing with the general form:
f(x) = ax2 + bx + c
f(x) = x2 − 4x + 3
Here a = 1
og b = −4
and c = 3 (so the graph crosses the y axis in 3).
Look at the rule for squaring a bracket:
(x ± q)2 = p2 ± 2xq + q2.
We see that the coefficient of x is 2q.
In our example the coefficient of x is −4 which means 2q = − 4 and therefore q = −2.
If we calculate (x − 2)2 we get x2 − 4x + 4.
(x − 2)2 = x2 − 4x + 4.
If we subract 1 from both sides
we get :
(x − 2)2 −1 = x2 − 4x + 4−1 = x2 − 4x + 3
Summarising the method:
| f(x) = x2 − 4x + 3 | Half the coefficient of x is −4/2 = −2 which we square (4 ) and add to the equation. |
| = (x2 − 4x + 22) − 22 + 3 | |
| = (x − 2)2 − 4 + 3 | If we
add 4 to the equation we must also subtract 4 so that the equation
remains unchanged Now we simplify −4+3 = −1 |
| = (x − 2)2 − 1 |
From the above example we can conclude that the graph of a second degree polynomial where a = 1 (f(x) = x2 + bx + c) has the axis of symmetry in:
x = −b/2 and cuts the y – axis where y = c.
Example 7
Find the axis of symmetry of the graph of f(x) = 2x2 − 12x + 10.
In this case a = 2 so the rule in the previous example does not apply. Neither is it as easy to rewrite the function as before.
Instead we translate the function down by 10 units by subracting 10 from the equation. Moving the graph vertically does not change the position of the axis of symmetry.
We call this new function g(x) and find where g(x) cuts the x axis.
2x2 − 12x = 0
2x(x − 6) = 0
This equation has the solutions x = 0 and 6 so the graph of g(x) cuts the x-axis in 0 and 6. The axis of symmetry must be in the middle of these two points, that is in x = 3.
Example 8
Rewrite the function f(x) = 2x2
− 12x + 10 in the form
f(x) = a(x + r)2 + s .
| f(x) = 2x2 − 12x + 10 | Take 2 outside a bracket.Half the coefficient of x is −6/2 = −3 so add 32 inside the bracket. We have really added 18 so now we have to subract 2×32 = 18 outside the bracket. |
| = 2(x2 − 6x + 32) − 2×32+ 10 | |
| = 2(x2 − 6x + 9) − 18 + 10 | |
| = 2(x − 3)2 − 8 |
Now we see, as before, that the axis of symmetry is in x = 3.
The coefficients of x In the above example (f(x) = 2x2 − 12x + 10) are a = 2, b = −12 and c = 10. In order to find the axis of symmetry we took the factor 2 outside a bracket. This corresponds to dividing by 2. Then we completed the square by dividing the coefficient of x (−6) by 2.
The general formula for the axis of symmetry of
the function
f(x) = ax2
+ bx + c is
therefore:

Example 9
Find the vertex of the parabola f(x) = 2x2 − 12x + 10.
The vertex (where the parabola turns round) lies on the axis of symmetry therefore we know the x-value of the vertex (3).

We find the y-value by calculating f(3).
f(3) = 2×32 − 12×3 + 10 = 18 − 36 + 10 = −8.
The vertex of the parabola is (3, −8).
Note: If a>0 the vertex is a minimum point. If a<0 the vertex is a maximum point.
Try Quiz 3 on Functions I.
Remember to use the checklist to keep track of your work.