© 2007  Rasmus ehf    og Jóhann Ísak

Sets I

 Print

 

Lesson 2

  Numerical sets

 

Several numerical sets (that is sets of numbers) are frequently used in mathematics. Here is a diagram showing the relation between them.

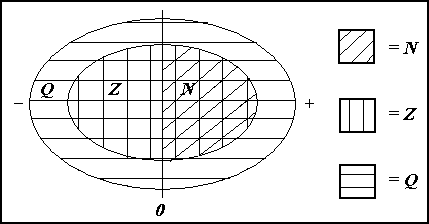
The simplest set is the set of Natural Numbers. The letter N is always used when talking about this set. N = {1,2,3,∙∙∙}. These are the numbers we use for counting and they carry on infinitely. Zero is often included in this set . This is shown by putting 0 as a subscript on the N.  N0 = {0,1,2,3,∙∙∙}.

The letter Z is used to symbolise the set of all the whole numbers, positive and negative.  Z = {∙∙−2,−1,0,1,2,∙∙}.

The set N is a proper subset of Z.

N Ì Z

The third set we mention is symbolised by the letter Q from the word Quotient. This is the set of all the rational numbers, or, in other words. The set of all fractions that can be written with whole numbers in the numerator and the denominator. Note that all whole numbers can also be written as fractions so Z and N are both proper subsets of Q.

Z Ì Q og N Ì Q

Notice that all the elements in these three sets can be written using whole numbers.  

Now we will consider some decimals.

Example 1

Write

and

 as decimals

Using a calculator and dividing 1 by 3 we get

0.333∙∙∙∙

and 4 divided by 33 gives

0.1212∙∙∙∙

The decimals in these examples have an infinite number of digits after the decimal point. The same sequence of digits repeats itself again and again. They are called periodic decimals.

In the first example the period is one digit, the number 3. In the second example the period consists of two  digits (1 and 2 are repeated). All rational numbers can be written as periodic decimals.

These examples show how a fraction can be changed into a decimal by division. Now we will see how a decimal can be changed into a fraction.

If the decimal  has a fixed number of digits then we can change it into a fraction by moving the decimal point until we have a whole number and then dividing by 10, 100, 1000... depending on by how many places we moved the decimal point

Example 2

Write 0.3, 0.12 and 0.1212 as fractions.

0,3

=

=

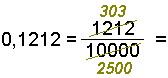This method doesn’t work with periodic decimals that have an infinite number of digits after the  decimal point. In that case we have to use another method.

Example 3

Change 0.333∙∙∙∙∙, 0.1212∙∙∙∙∙ and 1.14333∙∙∙ into fractions.

 

 

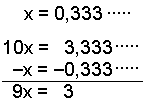Call the number x. When the period consists of one digit we multiply the number by 10 making 10x.

Now subtract the original number from 10x. 

In this way all the numbers after the decimal point cancel out. 

Finally divide the answer by 9 to find x. Cancel if possible.

 

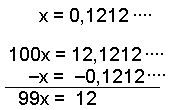Call the number x. This time the period has two digits so we multiply the number by 100  making 100x.

Now subtract the original number from 100x.

 

 

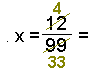
 Again all the numbers after the decimal point cancel out. 

Finally divide the answer by 99 to find x. Cancel if possible.

 
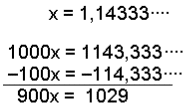In this example we have to start by multiplying by 100 so that the period starts straight after the decimal point. 

This time the period is only one digit so we multiply again by 10. 

Now we subtract 100x from 1000x so that the numbers after the decimal point cancel out.

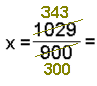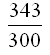Finally we divide and cancel to find the original x.

 

Try Quiz 2 on Sets I.  
Remember to use the checklist to keep track of your work.