© 2007  Rasmus ehf    og Jóhann Ísak Pétursson

Factorising polynomials

 Print

 

Lesson 1

Polynomial division and the Remainder Theorem.

Consider the function  f(x) = 6x2 − 9x + 3 and choose a few values of x to make a table of values. Imagine that we 

have been lucky enough to choose x = 1 and see that f(1) = 0. 

 

If x = 1 then (x − 1) = 0 .

The fact that f(1) = 0 tells us that (x − 1) is a factor of f(x).

If we assume (x−1) is a factor of f(x) we can also show that
f(1) = 0:

f(x) = 6x2 − 9x + 3 = (unknown factor)(x − 1)

  f(1) = 6 − 9 + 3 = (unknown factor)(1 − 1) = (unknown factor)∙0

         = 0

Now we need to divide 6x2 − 9x + 3 by  x − 1 to find the unknown factor.

We will now learn how to do this by comparing polynomial division to the way you have learned to do ordinary 

numerical division.

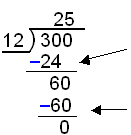
Example 1

Numerical division: 

How often does 12 divide into 30?
The answer is 2. Now multiply 2×12 = 24.
Subract 24 from 30 and move the 0 down.


How often does 12 divide into 60?
5 times.  5×12 = 60.
Subract 60 from 60

Polynomial division:

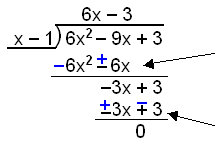How often does x − 1 divide into 6x2 ?  We only need to ask how often does x divide into 6x2, or what do we have to multiply x by to get 6x2.  The answer is 6x. Now multiply 6x∙(x − 1) = 6x2 − 6x.
Subtract 6x2 − 6x by changing the signs in front of each term.
 Next move 3 down. Now divide x−1 into −3x or ask what do we have to multiply x by to get −3x?  −3×(x − 1) = −3x + 3.  Subtract −3x + 3 by changing the signs. The remainder is 0.

f(x) = 6x2 − 9x + 3 can now be fully factorised:

f(x) =  (6x − 3)(x − 1) = 3(2x−1)(x − 1).

Example 2

We can also factorise 6x2 − 9x + 3 by using the formula for

quadratic equations to solve the equation 6x2 − 9x + 3 = 0. 

The coefficients are  a = 6, b = −9 and c = 3.

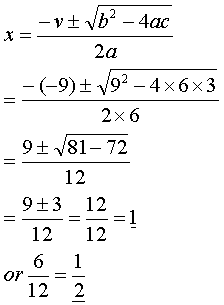
The solutions of the equation are x = 1 and x = ½  so the brackets (x − 1) and (x − ½) must both be

factors of 6x2 − 9x + 3. We get the following:

    6x2 − 9x + 3 = 6(x − 1)(x − ½).

We must have  6 as a factor in order to get the correct result when we multiply the factors together.

This example gives us a rule for factorising quadratic functions that can be factorised into two brackets:

ax2 + bx + c = a(x − r1)(x − r2)

The values r1 and r2  are called the ROOTS of the function  and are found by solving the corresponding quadratic 

equation.

 

 

Example 3

We will now divide x3 − 6x2 + 11x − 6 by x − 1 and use the result to factorise the polynomial.

 

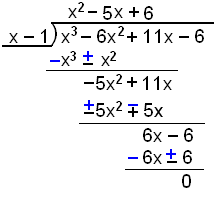x divided into x3  gives x2 because x must be multiplied by  x2 to get  x3.   

x2(x − 1) = x3 − x2. Subtract  x3 − x2 by changing the signs.

 Move 11x down. x divided into −5x2 gives −5x.  −5x(x − 1) = −5x2 + 5x.

Subtract  −5x2 + 5x  by changing the signs. Move −6 down.  x goes 6 times into 6x.    6(x − 1) = 6x − 6. Subract

The remainder is 0 which means that (x−1) is a factor of the polynomial. We can factorise the quadratic factor by 

inspection or any other method we have previously studied.

x3 − 6x2 + 11x − 6 = (x2 − 5x + 6)(x − 1) = (x − 3)(x − 2)(x − 1)

 

Example 4

Now we’ll look at a more difficult example.

Divide the polynomial x3 − 4x + 3 by x − 1 and then factorise

 

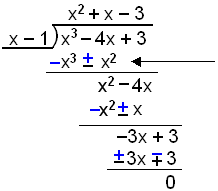In this case we cannot subtract   x2 and −4x,

so both terms remain unchanged.

 

The remainder is 0 so x − 1 is a factor. It now remains to factorise x2 + x − 3. It can’t be done by inspection ( trial and error ) so we have to use the quadratic formula.

  The coefficients are a = 1, b = 1 og c = −3.

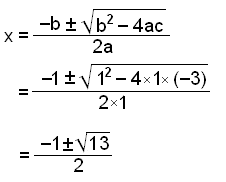
Fully factorised the polynomial will be:

x3 − 4x + 3 = (x2 + x − 3)(x − 1)

 

Example 5

Now we’ll look at an example where the remainder is not 0.

Divide x3 + 4x2 + x + 1 by x + 1.

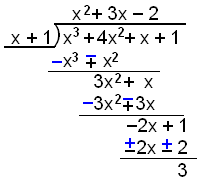
In this example the remainder is 3.

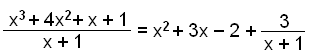
We can now rewrite the polynomial as:

This way of writing the outcome is important in what follows:

From this example we can see the following general result:

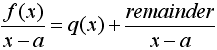
Where f(x) is a polynomial that is divided by (x−a) and q(x) is the outcome of the division (quotient).

If we multiply both sides of this equation by x − a we get

    f(x) = q(x)(x − a) + remainder

Now we will use this version of f(x) to calculate f(a).

    f(a) = q(a)(a − a) + remainder

    f(a) = q(x)∙0 + remainder

    f(a) = remainder

This shows us that we can find the remainder when a polynomial is divided by x−a without doing any division.

This is called The Remainder Theorem and says the following:

  If the polynomial f(x) is divided by  x − a then the remainder

   is f(a).

 

Example 6

Use the Remainder theorem to find the remainder when x3 + 4x2 + x + 1 is divided by x + 1.

If we can rewrite x + 1 as x−(−1) we can use the remainder theorem with a = −1.

    f(−1) = (−1)3 + 4×(−1)2 + (−1) + 1

            = −1 + 4 − 1 + 1

            = 3

If you look at the previous example, Example 5, you will see that this agrees with the answer there.

Example 7

Finally we will use the Remainder theorem to find the remainder when x3 + 4x2 + x + 1 is divided by x − 1.

We use the Remainder theorem with a = 1 and find the remainder when  x3 + 4x2 + x + 1 is divided by x − 1 by calculating f(1).

    f(1) = 13 + 4×12 + 1 + 1

          = 1 + 4 + 1 + 1

          = 7

Try Quiz 1 on Factorising polynomials.  

Remember to use the checklist to keep track of your work.