Exponentials and logarithms
| © 2007 Rasmus ehf and Jóhann Ísak Pétursson |
Exponentials and logarithms |
Lesson 2
Logarithms to the base of 10.
Few numbers are as easy to work with as 1, 10, 100, 1000 e.t.c. All we have to do if we wish to multiply them together is count the number of zeros.
E.g. 10×100×1000 = 1 000 000 , a total of 6 zeros.
We can also see this if we write the numbers as powers of 10.
10×100×1000 = 101×102×103 = 101+2+3 = 106 = 1000000.
About 400 years ago mathematicians had the idea that writing numbers as powers of 10 would make multiplication much easier. Instead of multiplying numbers together it would only be necessary to add the exponents. In the days before calculators anything that made calculations easier was very welcome.
A function that was called the logarithm was defined, written f(x) = lg x or f(x) = log x where log a is the power that 10 has to be raised to in order to equal a.
The function f(x) = log x is defined for all positive numbers and finds the power to which 10 has to be raised to give us x. We can only find the logarithm of positive numbers as powers of 10 are always poisitive.
The Domain
of the function f(x) = log x is therefore
{ xÎR | x
> 0 }.
We will now look at some logarithms on a calculator. This function can be found on all Scientific calculators but we will use the Casio graphical calculator.
To find log 2 you do the following:

![]()
f(1) = log 1 = 0 because 100 = 1
f(2) = log 2 ≈ 0.303 because 100.303 ≈ 2
f(3) = log 3 ≈ 0.477 because 100.477 ≈ 3
f(10) = log 10 = 1 because 101 = 10
f(20) = log 20 ≈ 1.303 because 101.303 ≈ 20
f(100) = log 100 = 2 because 102 = 100
f(1000) = log 1000 = 3 because 103 = 1000
The function f(x) = log x is the inverse of the function g(x) = 10x meaning that if one function is used on the outcome of the other then we get back the original number. This is the same idea as squaring a number and then taking it’s square root.
Example 1
 |
We take the log of both sides of the equation. As
the functions log x and |
Example 2
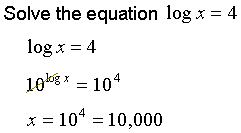 |
We
make both sides of the equation into powers of 10.
The functions log x and 10x cancel each other out and we are left with just x on the left side of the equation. |
Logarithms are simply exponents ( indices ) or powers and therefore follow rules corresponding to to the rules for indices.
We know that 10x×10y = 10x+y so it follows that if
x = log a and y = log b.
then log ab = log a + log b.
In the same we see that log a/b = log a − log b.
We can write log an = log a + log a + ∙ ∙ ∙ ∙ + log a
(n terms) = n log a.
This gives us the following logarithm rules:
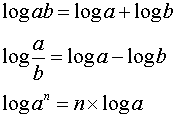 |
Example 3
The logarithm rules are used to combine the following into one logarithm term:
a) log a + log b + log c = log abc
b) log a + log 2b + log 3c + log 4 = log a×2b×3c×4 = log 24abc
c) log a + log a + log a = 3 log a = log a3
d) log 2a − log 2b = log 2 + log a − log 2 − log b = log a/b
e) ¼×(log a + log a3) = ¼×(log a + 3 log a) = ¼∙4 log a = log a
Example 4
Solve the equation by writing the left hand side of the equation as one logarithm.
a)
|
|
We
begin by using the log rules to change the left hand side from addition
and subtraction to multiplication and division. We then put in the base 10 on both sides of the equation. The 10 and log cancel each other out leaving us with 10x. Finally we divide
by 10 to find x. |
b)
|
|
Write both sides as exponentials with base 10.
|
c)
|
|
First
simplify.
Write both sides as exponentials with base 10.
|
d)
|
|
First
simplify.
Write both sides as exponentials with base 10.
|
The correct solution is x = 5 because log(-5) does not exist.
The rule log an = n log a is used to solve equations of the type ax = b, where the exponent is the unknown value.
We take the logarithm of both sides of the equation and then use this rule to move the x down.
ax = b
log ax = log b
x log a = log b
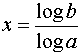
Example 5
| Solve the equation
2x = 8192. |
|
| log 2x = log 8192 | Take the log of both sides of the equation |
| x log 2 = lgo 8192 | and move the x down in front of the log as the rule says. |
| x = log 8192/log 2 = 13 |
Divide both sides of the equation by log 2 to give a value for x. |
Try Quiz 2 on Exponentials and logarithms.
Remember to use the checklist to keep track of your work.