© 2007  Rasmus ehf  and Jóhann Ísak Pétursson

Roots

Print

Lesson 1

Square roots

If we take the square root of a number and then take the square of the outcome, we get the original number back again. 

    e.g. 4 = 2 and 2² = 4.

We can say that the square root and the square cancel each other out. They are the inverse of each other.

If we have a number written with the index 2 ( squared) then taking the square root simply means that we leave out the 2 ( this only applies to positive numbers ).

We can therefore take any squared numbers that are under the square root sign out from under the root sign by leaving out the power 2.

Example 1

Simplify the following by taking the biggest possible value out of the square root.:

a)

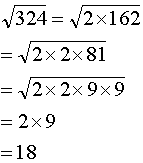We begin by factorising the number under the root sign. Both 2 and 9 appear twice. Therefore taking the square root leaves us with just 2 and 9 .  In the second example only 9 appears twice so 3 has to remain under the root.

b)

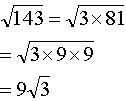
c)

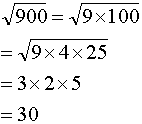
d)

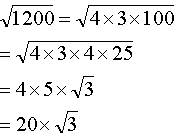
e)

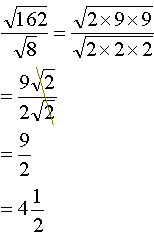
Most square roots are irrational numbers. This means we can’t give their exact value in  fractions or decimals.

Because of this, when we use calculators to find square roots we get only approximate values.  If we leave the square root in our calculations, we get what are called exact values.

When working with fractions and square roots it is customary to leave no square roots in the denominator.

Simplifying to remove square roots from the denominator is called “Rationalising the denominator”. In the simplest examples we just multiply the numerator and the denominator by the same square root.

Example 2

Rationalise the denominators in the following examples:

a)

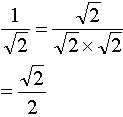Multiply the numerator and denominator by  Ö 2 . We then get (Ö 2)2 = 2 in the denominator.

b)

When we multiply two square roots togethe we can put both numbers under the same square root sign.

We could also do the problem like this:

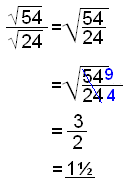Put both terms under the same square root sign and cancel.

If there are two terms in the denominator we use the rule about conjugate terms to get rid of the roots. (a+b) and (a−b) are conjugate terms and:

    a² − b² = (a + b)(a – b)

We multiply the numerator  and the denominator by the conjugate of the denominator, 

i.e. either by  (a − b) or by (a + b).

Example 3

Rationalise the denominator:

a)

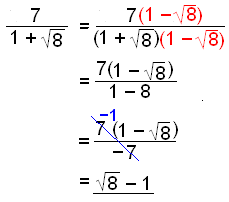The conjugate of    is

b)

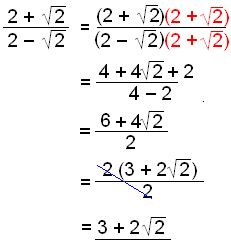
Try Quiz 1 on Roots.  

Remember to use the checklist to keep track of your work.