Roots
| © 2007 Rasmus ehf and Jóhann Ísak Pétursson |
Roots |
Lesson
2
Roots and powers
We are now going to look at the relationship between powers and roots.
| We know that 2×2 = 22= 4 |
and therfore |
| Also that 2×2×2 = 23 = 8 |
and therfore
3 |
| The 3 before the root sign means we are taking the cubic root. |
|
Note that when we take the square root we do not put in a 2.
Examples:
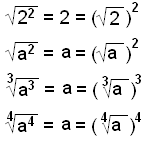
The second and fourth examples are only true if a is not negative.
Roots and powers are inverse operations like for example multiplication and division ( if you multiply by a number and then divide by the same number it’s as if nothing has happened).We could say they cancel each other out.
The equation (a2)x = a has only one solution for x, that is x = ½ so we conclude that taking the square root and raising to the power ½ is the same operation.
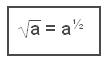
Using cubic roots we get:
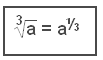
Generalising for any root:
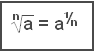
Changing roots to fractional powers and using the rules for exponents can make many calculations easier:
Example 1
Simplify the following as much as possible giving the answer as a single power:
a)
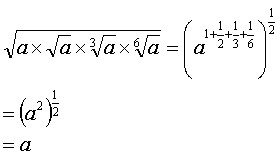 |
Change all the roots to fractional powers and add together the indices under the root sign. Then multiply by 1/2 |
b)
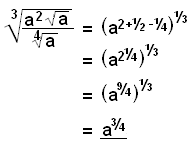
To solve an equation like
![]()
We raise both sides of the equation by the power b/a.
Example 2
Solve the following equations:
a)
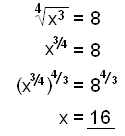 |
When we raise both sides to the power 4/3 we are left with x to the power of one. |
b)
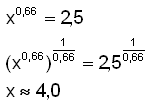 |
Here we use the power
|
This method is very easy to use but we have to take care when using it because there can be instances when it gives us the wrong answer.
When we raise to powers that are even (2, 4, 6, and so on) all negative values become positive and we have to check that our answers are correct by putting the answer back into the original equation.
Example 3
Let’s look at the following example:
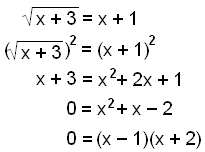
We get the solutions x = 1 and x = −2. Now let’s check them:
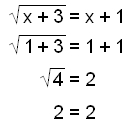
The solution x = 1 is correct.
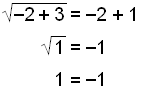
The solution x = −2 is incorrect. We lost the minus on the left hand side of the equation when we squared it.
Sometimes both solutions are correct. Look at the next example.
Example 4
Solve for x:
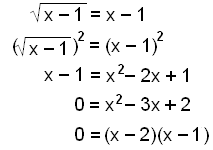
This gives the solutions x = 1 and x = 2.
Checking the answers we get:
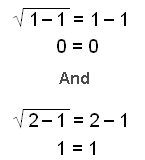
Which are both correct .
Try Quiz 2 on Roots.
Remember to use the checklist to keep track of your work.