Math Scene - Inequalities - Lesson 1 - Solution of inequalities

Solving an inequality involves finding a number or an interval of the real numbers that satisfy a given condition.This condition is given by using any of the following inequality symbols:

The statement 3 > 2 (three is greater than two) is a true statement. If you have a problem remembering which way the sign turns then try to remember that the arrow points to the smaller number. The statement 2 < 3 (two is less than three) is also true.

When we say that x > 2 we mean that x is a real number greater than two. Using Set notation we write {x

R | x > 2} to emphasize the fact that x is any real number.

The notation x

2 means that x is any real number greater than or equal to 2. The difference being that now we include 2.

We can often use the same methods to solve inequalities that we use to solve equations. We can, for example, add or subtract the same number from both sides of an inequality in the same way as with equations. We can also multiply and divide both sides by the same number but only if we use positive numbers.

Example 1

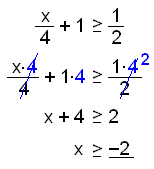We multiply every term by 4 to get rid of the fractions.

We then subtract 4 from both sides of the inequality.

This example shows an inequality that can be solved in exactly the same way as if it were an equation. Unfortunately this is not always the case. The exceptions occur when we have to multiply or divide by negative numbers. Look at the following diagram:

We can see from the real number line that a < b. If we multiply by −1 we would get −a < −b. If we look at the real number line we see that this is no longer true as −a is to the right of −b and therefore −a > −b .

This lead to the rule that if we multiply by a negative number we have to turn the inequality sign round.

Example 2

2 − x > 1

−x > −1

x < 1

Subtract 2 from both sides.

Now multiply through by −1, remembering to turn the inequality sign round.

When solving equations we can turn both sides of the equation up side down, so that the numerator and denominator change places. ( e.g a/x=b/c can be written x/a = c/b ). This is no longer possible when working with inequalities

If a < b then 1/a > 1/b because when we divide by the bigger number the outcome gets smaller. We can do this however as long as we remember to turn the inequality sign round.

Example 3

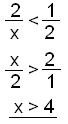We turn the fraction on both sides of the inequality sign round and reverse the inequality sign.

Finally we multiply through by 2.

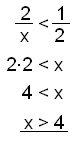
There are other calculations that we have to beware of when solving inequalities. For example we can’t square both sided of an inequality if one of the terms is negative. This is the same as multiplying by a negative number. We have to be very sure that the functions we are working with are increasing on the interval we are working with before we can treat inequalities in the same way as equations.

But what is meant when we say a function is increasing? Below are three graphs that we are going to use to solve inequalities.

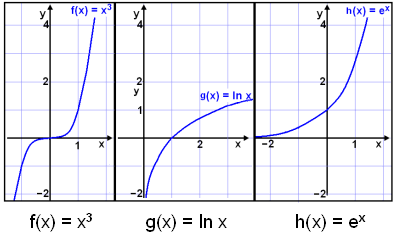
The functions f(x) = x³, g(x) = ln x and h(x) = e^x are all increasing. This means that as x increases the function increases. When we move along the graph from left to right the graph goes up. As we have seen before the function g(x) = ln x is only defined for positive x – values .

Example 4

Example 5

Again there is no problem here. We raise both sides to the power of e to get rid of the ln − function. We then get :

Example 6

e^x > e^−x

(e^x)² > 1

e^2x > 1

2x > 0

x > 0

Multiply both sides by ex to get rid of e^−x or 1/e^x on the right hand side.

Then put ln on both sides of the equation to cancel out the e.