| © 2008 Rasmus ehf and Jóhann Ísak | Triangles |
|
In lesson 2 we found the rule
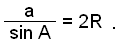
This rule also holds if we use angles
B or C and sides b or c instead of angle A and side a.
This leads to the following rule called the Sine Rule:
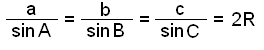 |
We use this rule to find unknown angles and sides in a triangle when we know one angle and the side opposite to that angle together with either one other side or angle.
This is the basic rule used in land measurement and map making. We can rewrite the rule in three parts to use depending on the sides and angles that are known.
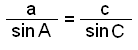 |
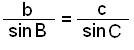 |
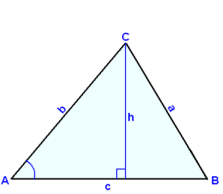
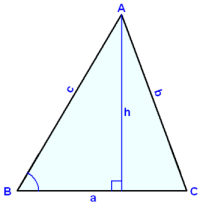
The following diagrams show the same triangle standing on each of the three sides in turn. We can write a formula for the area in each case using different bases and heights.
 |
 |
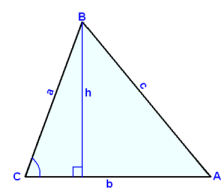 |
F = ½×c×h F = ½×a×h F = ½×b×h
Using the rule sin x = opposite side/hypotenuse we get
sin A = h/b sin B = h/c sin C = h/a
h = b×sin A h = c×sin B h = a×sin C
The area of the triangle is therefore:
| F = ½ ×c×b×sin A F = ½×a×c×sin B F = ½×b×a×sin C |
The area F is of course the same in each case and we can use these formulas to write the sine rule in another way. We divide all through by ½×a×b×c.
½×b×c×sin A = ½×a×c×sin B = ½×a×b×sin C = F
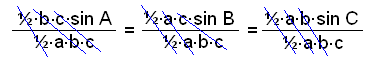
Leading to the sine rule written as:
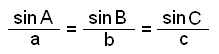 |
Example 1
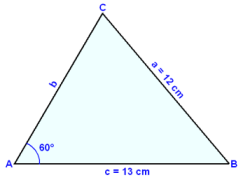
In an acute angled triangle side a = 12 cm, side c = 13 cm and angle A = 60°. Find angle C, side b and the area of the triangle.
First we draw and label a diagram .
Next we use the sine rule to find angle C.
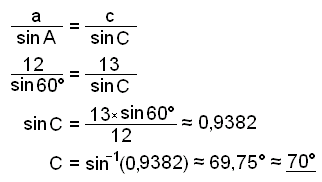
B ≈ 180° − 69,75° − 60° ≈ 50,25° ≈ 50°
Next we use the rule to find side b.
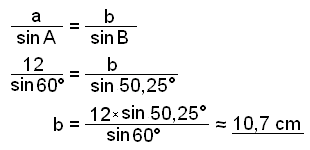
Finally we use the area rule to find the area F.
F = ½×b×c×sin A ≈ ½×10,7×13×sin 60° ≈ 60 cm 2
Example 2
In an obtuse angled triangle side a = 12 cm, side c = 13 cm and angle A = 60°. Find angle C, side b and the area of the triangle.
This is the same example as above except that one angle of the triangle is obtuse
( greater than 90°).
When we found angle C in example1 above we assumed that the calculator gave us the correct answer. The calculations were as follows:
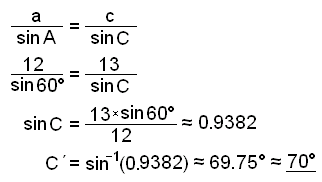 |
sinC = 0,9382 |
We are told this triangle has an obtuse angle so we need to remember the rule that gives us the second solution to the equation. The rule is:
sin v° = sin (180° − v°)
This gives us the obtuse
angle C ≈ 180° − 70° ≈ 110°
and therefore the angle B ≈ 180° − 60° −
110° ≈ 10°
But how can we explain that there can be two different triangles with the given measurements? Look at a diagram
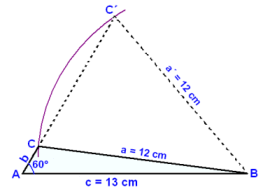
First we draw the base line c = 13 cm. We then draw an angle of 60° at one end of the base line and label it A. Label the other end of the base line B. Using B as the centre, we draw a circle of radius 12 cm. This circle cuts the arm of the angle A in two places telling us that there are two possible positions for the point C. One leads to an acute angled, the other to an obtuse angled triangle ( see the diagram).
We now continue with example 2 and find side b.
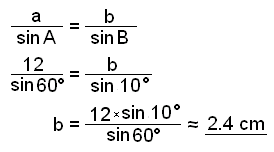
Finally we calculate the area of the triangle.
F = ½×b×c×sin A ≈ ½×2,4×13×sin 60° ≈ 13,5 cm 2
Example 3
In an obtuse angled triangle side a = 15 cm, side c = 6 cm and angle A = 60°. Find angle C and side b.
Draw and label a triangle.
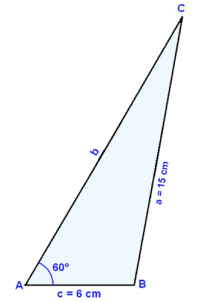
Use the Sine rule.
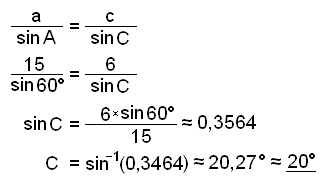
B ≈ 180° − 60° − 20,27° ≈ 99,73° ≈ 100°
Find side b.
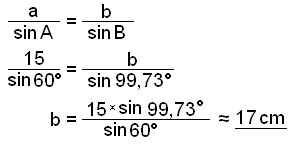
These calculations agree with the diagram. There is no other triangle that satisfies the given measurements.
From the above examples we can draw the following conclusions:
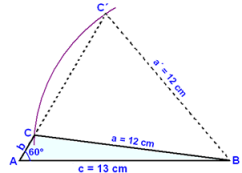
| When the side opposite the given angle is shorter than the side adjacent to the angle (the base line) we need to know whether the triangle is acute or obtuse. If we do not have this extra information then there are two possible triangles and therefore two sets of solutions. |
Example 4
In triangle ABC, side c = 12 cm, angle A = 60° and angle B = 80°. Find the sides b and c.
Draw a diagram with c = 12 cm as the base line. We can easily find the third angle in this triangle and if we know all the angles there is only one possible solution.
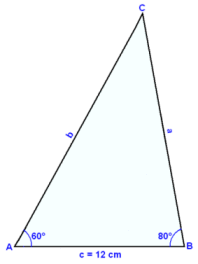
First we need to find angle C.
C = 180° − 60° − 80° = 40°
Now we use the Sine rule to find the side a.
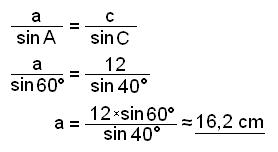
Finally we find side b.
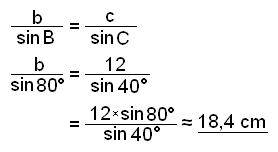
We can always use the Sine rule to find
unknown sides and angles in a triangle if we are given one side and two angles.
(see example 4).
We can also use the Sine rule if we know two sides and the angle opposite one of
the sides (see examples 1-3). In this case we need to know whether the triangle
is obtuse or acute angled.
But what about triangles where we know two sides and
the angle between them, or only three sides and no angles?
We can easily draw a triangle if we are given this information and therefore it
should be possible to calculate the unknown angles and sides. The Sine rule
doesn’t work so we need to find some other method.

We draw and label a triangle ABC and divide it into two right angled triangles by drawing in the height h. Now we use Pythagoras rule in both of these triangles.
h2 = a2 − x2 and h2 = c2 − (b − x)2 = c2 − b2 + 2×b×x − x2
Equating these two equations we get
c2 − b2 + 2×b×x − x2 = a2 − x2
Solve this equation for c2.
c2 = a2 + b2 − 2×b×x
Now we get rid of the x in the formula using the rule
cos C = x/a which gives us x = a cos
C.
Putting this into the formula instead of x gives the following formula:
| c2 = a2 + b2 − 2×b×a×cos |
This formula is know as the Cosine Rule and can be used to find side c if we know sides a and b and the angle between them, angle C (see the above diagram).
It can be proved that the Cosine rule also holds for obtuse angled triangles. The proof is very similar to the proof of the rule for acute angled triangles.
If we use other angles and sides we get the following equivalent formulas:
| a2 = b2 +
c2 −
2×b×c×cos
A
b2 = a2 + c2 − 2×a×c×cos B |
If all the sides of a triangle are known we can use the Cosine rule to find the angles. For example if we want to find angle C we solve the formula for cos C and then use calculators to find the angle.
c2 = a2 + b2 − 2×b×a×cos C
2×b×a×cos C = a2 + b2 − c2
Dividing by 2ab we get the following:
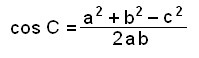 |
The equivalent formula for the other angles are:
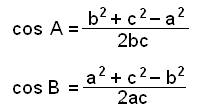 |
Example 5
In triangle ABC the side c = 12 cm and b = 15 cm. Angle A which lies between sides b and c is 60°. Find side a,angle C and the area of the triangle.
First draw and label a diagram.
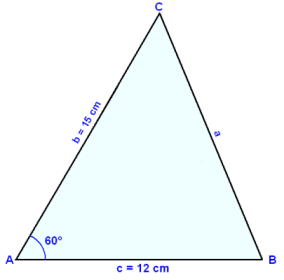
Using the Cosine rule for cos A.
a2 = b2 + c2 − 2×b×c×cos A
= 152 + 122 − 2×15×12×cos 60°
= 225 + 144 − 180 = 189
![]()
Now we can use either the Sine or Cosine rule to find angle C. We will use the Sine rule.
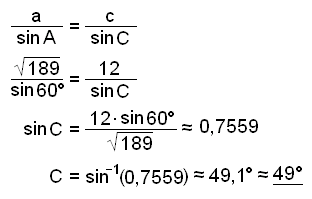
Finally we find the area.
F = ½×b×c×sin A ≈ ½×15×12×sin 60° ≈ 78 cm2
Example 6
In triangle ABC, a = 12 cm, b = 11 cm and c = 13 cm. Find the area of the triangle.
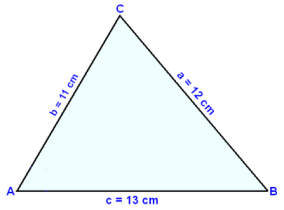
Before we can find the area we need to find one angle. We’ll use the Cosine rule to find angle C.
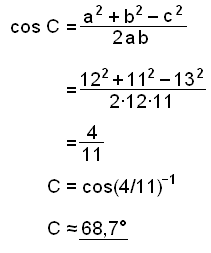
Now we can find the area of the triangle
F = ½×a×b×sin
C ≈ ½×12×11× sin 68,7° ≈ 61,5 cm2
Try Quiz 3 on Triangles.
Remember to use the checklist to keep track of your work.