© 2008  Rasmus ehf    and Jóhann Ísak

Trigonometry Rules

Lesson 1    Pythagoras rule for Cosine and Sine

Mathematics has many rules that help us  to simplify and there by solve the  more complicated trig equations.

We are now going to find and use one of them, probably the most useful one of all.

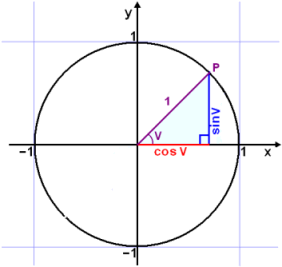
This rule is often called Pythagoras rule for sines and cosines. The diagram  shows a right angled triangle drawn in the unit circle. Pythagoras rule is true for all points  P is on the unit circle.

This means that
(sin v)2+(cosv)2=1. 

This rule is usually written in the form:

sin 2 v + cos 2 v = 1

It can be rewritten in two ways:

sin 2 v = 1 − cos 2 v

and

cos 2 v = 1 - sin 2 v

Example 1

Find sin x if cos x = ⅓ and 0 x <  

(x is an angle between 0° and 90°).

We can solve this problem using a calculator,
cos −1 (⅓) ≈ 70.53° and therefore sin 70.53° ≈ 0.94. If we want an exact answer we can do this example without a calculator, using Pythagoras rule.

Example 2

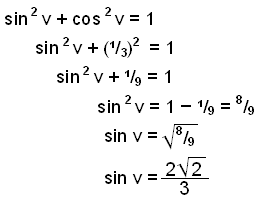
Use the rule  sin 2 v + cos 2 v = 1 to find other ways of writing the expression 1/ cos 2 v.

One way is by moving sin 2 v over the equals sign, so that we get cos 2 v = 1 − sin 2 v and then inverting both sides of the equation. This gives us

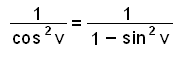
There’s another, not so obvious way, that leads to an expression that can often be useful. Look what happens if we  divide the original equation,  sin 2 v + cos 2 v = 1, by cos 2 v.

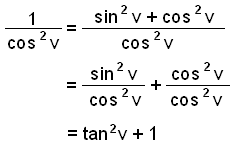
We have now proved the rule:

Example 3

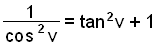
We will now use Pythagoras for trig functions to find the value of, first sin 2 v then cos 2 v, given sin 2 v = cos 2 v.

We first replace cos 2 v using the rule cos 2 v = 1 − sin 2 v.

      sin2 v = cos2 v

      sin2 v = 1 − sin2 v

   2×sin2 v = 1

      sin2 v = ½

Now we replace sin 2 v using sin 2 v = 1 − cos 2 v.

          sin2 v = cos2 v

   1 − cos2 v = cos2 v

                 1 = 2×cos2 v

         cos2 v = ½

Example 4

Solve the equation cos 2 x = sin x + 1.

First replace cos 2 x.

        cos2 x = sin x + 1

   1 − sin2 x = sin x + 1

                0 = sin2 x + sin x = sin x (sin x + 1)

This leads to  sin x = 0 or sin x = −1, so that

x = k×p (k×180°) or x = 3p/2 + k×2p (270° + k×360°).

Example 5

Simplify the equation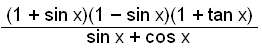

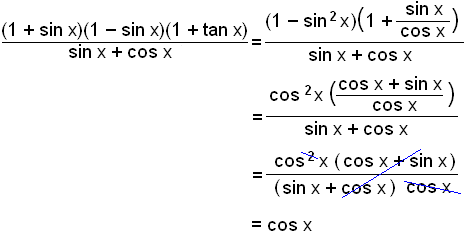Here we use the rule that  

(a + b)(a − b) = a2 − b2 and then rewrite  tan  x as í sin x/cos x before simplifying

Try Quiz 1 on Trigonometry Rules.

Remember to use the checklist to keep track of your work.