© 2008  Rasmus ehf  and Jóhann Ísak

Trig Formulas

Lesson 2  

The formulas for the sines, cosines and tangents of the sum or difference of two angles can be very useful. A proof of some of the rules is given here.

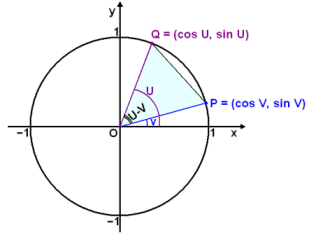
The triangle OPQ in the diagram has vertexes P, Q and O, the centre of the coordinate system. We will call the angle between the x-axis and OQ u, and the angle between the x-axis and  OP v. The angle POQ is therefore u − v. The point Q has coordinates (cos u, sin u) and the point P has coordinates (cos v, sin v). The distance between P and Q can be written |PQ| . We now use the formula for the distance between two points to find this distance.

   |PQ|2 = (cos u − cos v)2 + (sin u − sin v)2  

            = cos2u − 2 cos u cos v + cos2v

               + sin2u − 2 sin u sin v + sin2v  

            = 1 − 2 cos u cos v− 2 sin u sin v + 1

            = 2 − 2 cos u cos v − 2 sin u sin v

(distance)2 =

(x2−x1)2 + (y2−y1)2

Multiply out of the brackets and simplify.

Now we find |PQ| using the cosine rule.

   |PQ|2 = 12 + 12 − 2×1×1×cos (u − v)

             = 2 − 2×cos (u − v)

Equating these two expressions we get:

   2 − 2×cos (u − v) = 2 − 2 cos u cos v − 2 sin u sin v

     − 2×cos (u − v) = − 2 cos u cos v − 2 sin u sin v

If we divide all through by −2 we get the following formula:

cos (u − v) = cos u cos v + sin u sin v

We get a second formula from this one by putting −v in the formula instead of v:

   cos (u − (−v)) = cos u cos (−v) + sin u sin (−v)

Using the rules we found from the unit circle, cos (−v) = cos v and sin (−v) = − sin v we can rewrite this expression as:

cos (u + v) = cos u × cos v − sin u × sin v  

In the diagram below we have drawn two triangles. One  has an angle v between the hypotenuse and the x-axis, the other has the same angle between the hypotenuse and the y-axis. This means that the two triangles are congruent ( exactly the same).

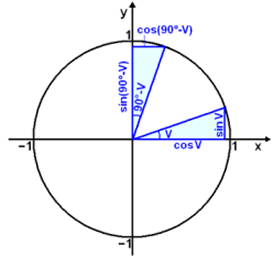
These congruent triangles lead to the following rules:

   cos v  = sin (90° − v)    and   sin v = cos (90° − v)

We now substitute 90° instead of  u and (u + v) instead of v into these rules to get two formulas for sines. 

    sin (u + v) = cos (90° − (u + v))

                     = cos ((90° − u) − v)                                         

                 = cos (90° − u) cos v + sin (90° − u) sin v

                 = sin u cos v + cos u sin v

In this way we have found a formula for sin (u + v):

sin (u+v) = sin u cos v + cos u sin v We use the rula cos(u-v) = cos u cos v+sin u sinv and then sin v = cos (90° − v) and cos v  = sin (90° − v).

If we now substitute (−v) for of v in this formula, we get the following:

sin (u − v) = sin (u + (−v))

                    = sin u cos (−v) + cos u sin (−v)

                    = sin u cos v − cos u sin v

  

In this way we have found a formula for sin (u − v):

sin (u-v) = sin u × cos v - cos u ×sin v

By replacing v by u in the formulas sin (u + v) and cos (u + v) we get  formulas for sin (u + u) and cos (u + u), called the double angle formulas. These can be written:

sin 2u = 2 sin u × cos u

cos 2u = cos2 u − sin2u

The rule for cos 2u can be written in two more ways by using the rule cos 2 u + sin 2 u = 1. 

First we replace cos 2 u by using cos 2 u = 1 − sin 2 u and then sin 2 u using sin 2 u = 1 − cos 2 u, giving the formulas:

cos 2u = 2 cos2 u − 1

cos 2u = 1 − 2 sin2 u

Example 1

Use the above formulas to find exact values for sin 15°
and cos 15°.

We have already found that cos 45° = 2/2, sin 45° = 2/2,
cos 60° = ½ and sin 60° = 3/2. Using the formula for
cos (u - v) we get the following:

   cos 15° = cos (60° − 45°)

                 = cos 60° × cos 45° + sin 60° × sin 45°

                 = ½×2/2 + 3/2×2/2

                 = 2/4 + 3×2/4

                 = 2×(1 + 3)/4

Using the formula for sin (u - v) we get the following:

     sin 15° = sin (60° − 45°)

                 = sin 60° × cos 45° − cos 60° × sin 45°

                 = 3/2×2/2 − ½×2/2

                 = 3×2/4 − 2/4

                 = 2×(3 − 1)/4

Example 2

Simplify the expression sin (270° − v).

We use the rule sin (u − v) = sin u × cos v − cos u × sin v.

sin (270° − v) = sin 270° × cos v − cos 270° × sin v

                       = −1× cos v − 0× sin v         

                       = − cos v

sin 270° = −1

 cos 270° = 0

Example 3

Find a formula for cos 3x that only uses sin x and cos x.

We use the formula cos (u + v) = cos u × cos v − sin u × sin v and replace u
by 2x and  v by  x.

cos (2x + x) = cos 2x × cos x − sin 2x × sin x cos 2x = cos2x − sin2x     sin 2x = 2 sin x × cos x

                      = (cos2 x − sin2 x)×cos x − (2 sin x × cos x)×sin x

                      = cos3 x − sin2 x × cos x − 2 sin2 x × cos x

                      = cos3 x − 3 sin2 x × cos x

Example 4

Solve the equation sin 2x + 2 sin x = 0 on the interval

0 x < 2.
sin 2x + 2 sin x = 0  
2 sin x cos  x + 2 sin x = 0
2 sin x (cos  x + 1) = 0
sin x = 0 og cos x = − 1.

Use sin 2x = 2 sin x cos x.

One solution is sin x = 0

   x = 0 or (0° or 180°)

Another solution is  cos x = −1

   x = (180°)

The solutions are therefore 0, and .   

Example 5

Solve the equation 7 cos 2 x + 5 sin 2 x + 6 sin 2x = 0

First we use the formula sin 2x = 2 sin x × cos x.

   7 cos 2 x + 5 sin 2 x + 12 sin x × cos x = 0

An equation of this type, with two factors of sin or cos in each term can be solved by dividing through by cos2x and changing the equation into a tan-equation.

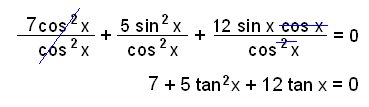
This is a quadratic equation with a = 5, b = 12 and c = 7.

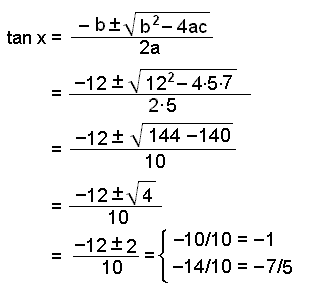
   tan x = −1 gives x = −/4 + k×  (−45° + k×180°)

   tan x = −7/5 does not give an angle that is an exact proportion of  .

         x ≈ −0.95 + k×  (54,5° + k×180°)

Try Quiz 1 on Trigonometry Rules.

Remember to use the checklist to keep track of your work.