Trig Rules
| © 2008 Rasmus ehf and Jóhann Ísak | Trig Rules |
|
Equations of the type a sin x + b cos x = c
The diagram shows the graph of f(x) = sin x + 2 cos x.
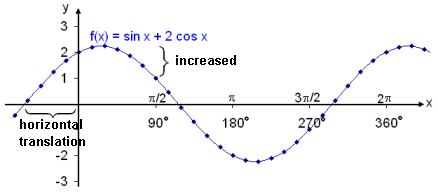
Amazingly it looks like an ordinary sine wave that has been translated to one side and with an amplitude that is bigger than that of the basic wave. We have seen before what affects the amplitude and how the amplitude can be increased from the value 1 by multiplying by a constant greater than 1. ( see trig functions lesson 3). We have also seen that the graph of the basic function can be translated horizontally by adding a constant to the angle. With this is mind we should be able to rewrite our equation in the form m sin (x + v), such that
m sin (x + v) = sin x + 2 cos x
Now look at the graph of g(x) = sin x − 2 cos x.
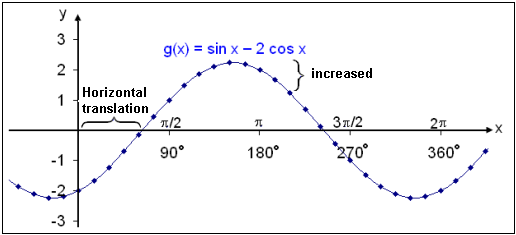
This is obviously the same curve except for the fact that the translation is now in the opposite direction to previously, translated to the right by the same length as the previous curve was translated to the left. In this case we should be able to form the equivalent equation.
m sin (x − v) = sin x − 2 cos x
We now rewrite these expressions using the addition formula:
sin (x + v) = sin x cos v + cos x sin v
sin (x − v) = sin x cos v − cos x sin v
Multiplying through by m we get:
m sin (x + v) = m sin x cos v + m cos x sin v
m sin (x − v) = m sin x cos v − m cos x sin v
Compare the result to the original equation.
m sin (x + v) = 1 sin x + 2 cos x
= m cos v sin x + m sin v cos x
m sin (x − v) = 1 sin x − 2 cos x
= m cos v sin x − m sin v cos x
We see that in both cases the following must be true:
m cos v = 1
m sin v = 2
If we divide the lower equation by the upper we get the following:
tan v = 2/1
Which gives the angle v = tan−1 (2) ≈ 63.4°.
If we draw a right angled triangle with the shorter sides1 and 2, the same values as are in the equation, then we can calculate the length of the hypotenuse and see that:
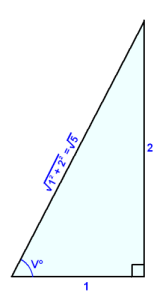
cos v = 1/
and sin v = 2/.
Using the equations
m cos v = 1
m sin v = 2.
Gives us that:
m×1/ = 1
m =
In other words we can rewrite the equation as:
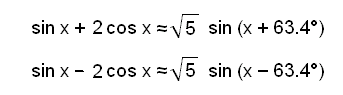
We see that the amplitude of the wave in the
functions
f(x) = sin x + 2 cos x and g(x) = sin x − 2 cos x is .
Generalising and using a and b for the constants
we get the following rule:
 |
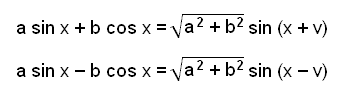The angle v can be found using:
| tan v = b/a where a > 0, b > 0 and 0° < v°< 90° |
Example 1
Find the amplitude of the function f(x) = 3 sin x + 4 cos x.
We begin by rewriting the function.
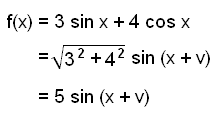
The amplitude is 5.
Example 2
The graph of the function f(x) = 3 sin x + 4 cos x is a sine wave that has been translated. Calculate by how many degrees and in which direction the wave has been translated.
f(x) = 3 sin x + 4 cos x
= 5 sin (x + v)
v = tan −1 (4/3) ≈ 53.1°
The wave has been translated
by 53.1° to the left
(f(x) ≈ 5 sin (x + 53.1°).
Example 3
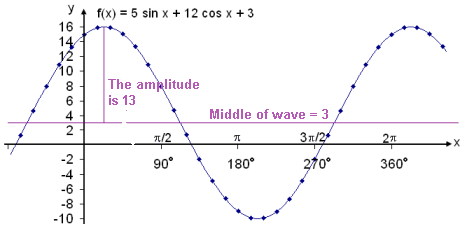
Given the function f(x) = 5 sin x + 12 cos x + 3. Find the amplitude, the maximum height and the translation of the wave.
Rewrite f(x).
tan −1 (12/5) ≈ 67.4°
f(x) = 13 sin (x + 67.4°) + 3
The amplitude is 13 so the maximum height is 13 + 3 = 16. Look at the graph.
Example 4
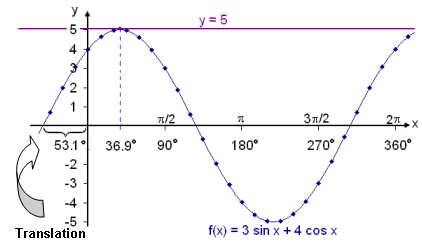
Solve the equation 3 sin x + 4 cos x = 5 on the
interval
0° 
x < 360°.
3 sin x + 4 cos x = 5
= 5 sin (x + 53.1°)
sin (x + 53.1°) = 5/5 = 1
x + 53.1° = sin −1 1 = 90° + k×360°
x = −53.1° + 90° + k×360°
x = 36.9°
This gives one solution 36.9° in the first quadrant.
It’s interesting to look at the graph. We see there is no other solution on the required interval.
Example 5
Find all solutions of the
equation sin x − 
3 cos x = 1.
We see that tan v =
3 and v = tan−1 (3) =
/3 (60°).
So sin (x −
/3) = ½
| (x −
/3) = sin −1 (½) =
/6 + k×2 |
|
x =
/3 +
/6 + k×2
=
/2 + k×2
Or a second possibility
(x −
/3) =
−
/6 + k×2
x =
/3 +
−
/6 + k×2
|
x = 7/6 + k×2 |
7 |
Try Quiz 1 on Trigonometry Rules.
Remember to use the checklist to keep track of your work.