© 2008 Rasmus ehf and Jóhann Ísak
Vectors
|
© 2008 Rasmus ehf and Jóhann Ísak |
Vectors |
|
Vector components
When a vector 
is
written as the sum of two vectors
and 
such
that
+ =
we
say that we have resolved (split) the vector
into
its components.
We
often resolve the vector into vertical and horizontal components as the diagram
shows, as these components are very important in physics when we are considering
forces.
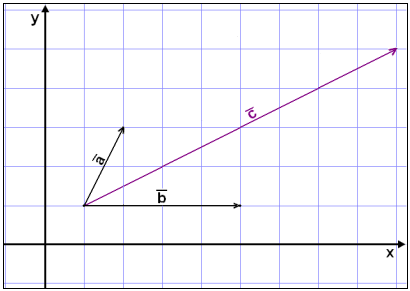
In general we can resolve a vector into components parallel to any two given
vectors. Below is an example you have seen before. We need to find the vector
,
using the vectors
and
,
in other words resolve the vector
into
components parallel to
and
.
Add another to
the one already in the diagram then add one and a half of vector
.
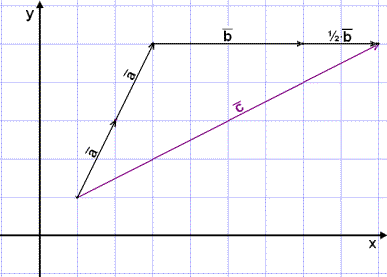
This shows us that the required components 2
and 1½ .
Any vector 
can be split
into unique components parallel to any non- parallel vectors and
as
long as neither has the length 0 (vectors
of length 0 are called zero vectors).
We do this by finding numbers t and r such:
= r×+
t×
We do this by calculating values for r and t that make the equation correct.
Resolve the vectors ,
and
in
the diagram into their vertical and horizontal components.
We use two vectors of length 1 ( one unit in the coordinate system ), one
vertical and one horizontal. These vectors are called unit vectors and are
usually written as
(
horizontal and therefore parallel to the x axis)
and
(
parallel to the y axis
).
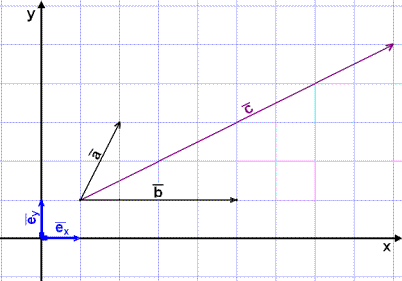
First we find the components of
.
It can easily be seen from the diagram that
=
+ 2.
We simply count the squares. The vector is
4 units to the right and
is
8 units to the right and 4 units up.
= 4
og
= 8
+ 4.
A force of 100 N acts at an angle of 25° to the horizontal. Find the vertical and horizontal components of the force.
A diagram helps us understand the problem.
We have a right angled triangle and can use
trig
rules
to find the magnitude of the components, that is
||
and ||
|
cos 25° =
adjacent side/hypotenuse
= |
|
Sin 25° =
opposite side/hypotenuse
= |
| |
Multiply through by 200. The absolute value symbol means the length or magnitude of the vector |
The horizontal component of a vector such as in the above
example is called the projection of the vector
on the x-axis.
The vertical component of a vector such as
in the above
example is called the projection of the vector
on the y-axis. You can see this on
the diagram below.
We can find a formula for the projection of a vector onto a horizontal line or vector. The formula is as follows:
|
Projection of
Projection of |
|
The vector
To begin with this doesn‘t look easy but the diagram helps to show how this problem can be approached. |
 |
We need to find vectors r×
and t×
which, when added together form the vector
 .
The diagram shows us that, when we add these vectors, we get a triangle
( blue in the diagram) with an angle of 30°(between
In other words, we know all the angles of the triangle and one side of
length 4 (| |
 |
 |
Here we use the sine rule
|
We can find t×||
in the same way.
We have calculated the lengths of the sides of the triangle, now we need to find the numbers r and t. We begin by finding r.
r×|
|
≈ 2.611
r×3 ≈ 2.611
r ≈ 2.611/3 ≈ 0.87
Then t.
t×||
≈ 1.786
t×5 ≈ 1.786
t ≈ 1.786/5 ≈ 0.36
The final result of resolving
in
components parallel to
and
is
therefore:
≈
0.87×
+ 0.36×
The above example ( example 3 ) shows how we can use the sine rule to resolve a vector into components parallel to two given vectors. All we need to know is the direction of the three vectors and the length of the vector we wish to resolve. This is a very useful method and is repeated in the frame below.
|
When we need to resolve a vector into two components parallel to given vectors we first draw a diagram and then use the sine rule. |
Resolving a vector into parts is much easier when we are working in a
rectangular coordinate system. In example 1 we introduced horizontal and
vertical unit vectors
and
.
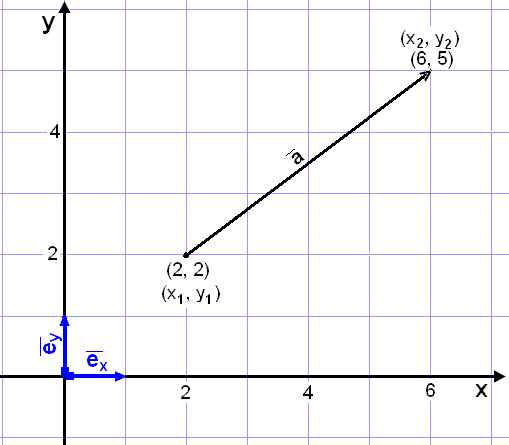
We can resolve the vector
in
the above diagram in the same way as we did in example 1. The result is:
= 4
+ 3
In order to get from the starting point (2, 2) to the end point (6, 5) we need
to move four squares horizontally to the right (4)
and three vertically up (3).
This shows us at once that the projection of the vector onto the x-axis is 4
and the projection onto the y-axis 3. This can easily be counted when working in
a coordinate system. We can also calculate this by finding the difference
between the starting and finishing points.
6 − 2 = 4 and 5 − 2 = 3
As you know we can place the vector anywhere in the coordinate system, length and direction is all that matters. Because of this it is convenient to place the vector with the starting point in the origin, the end point will then be in the point (4, 3).
The vector is then said to have coordinates
=
(4, 3).
Using coordinates for the vector in this way means that the vector can be placed anywhere in the coordinate system, the coordinates (4, 3) simply means that the vector has a direction that is 4 units horizontally and 3 units vertically.
The problem with writing vectors as coordinates in this way means that there could be confusion between coordinates of vectors and coordinates of points. Although some texts do write vectors in this way it is much more common to write the coordinates of a vector vertically to distinguish between coordinates of a point and coordinates of a vector.
We will therefore in this text write the vector
as:
The formula for the coordinates of a vector between two points is:
|
Coordinates of a vector = coordinates of the end point – coordinates of the starting point.
|
a)
Find the coordinates of
=
.
To go from A to B we simply move two squares horizontally to the right, neither up nor down. The x coordinate is therefore 2 and the y - coordinate 0.
Using the formula to calculate this we have to subtract. Coordinates of the end point (B) – starting point (A).
We have A = (1, 1) and B = (1, 3), which gives us
b)
Now find the coordinates of
=
.
A = (1, 1) and F = (4, 3), therefore
c)
What are the coordinates of +
?
If we add
and
together,
(by placing
at
the end
)
we end up at the point G and have moved, from start to finish, 5 units to the
right and 2 units up. To calculate this we add the x- coordinates together and
add the y coordinates together giving us:
d)
Now let’s find
−
.
If we turn
round
to make -
and then add
to
it we get the vector 
which
is goes 1 unit to the left and 2 units down. Calculating we get:
e)
Finally we will find the vector +
2.
Here we need to double and
add it to ,
taking us to the point M. Now we have moved 8 units to the right and 4 units up.
The calculation is as follows:
The above examples lead us to the following rules for adding, subtracting and multiplying vectors by a constant when we know their coordinates.
If the vectors
and
have
the general form:
and
then:
|
Addition:
Subtraction:
Multiplication by k: |
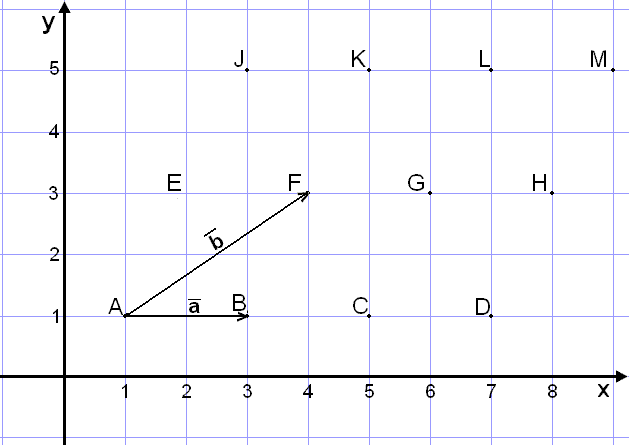
If we know the coordinates of vectors we can solve a problem similar to the one in example 3 without using trigonometry.
The vectors
,
and
have
the coordinates
and
(See diagram).
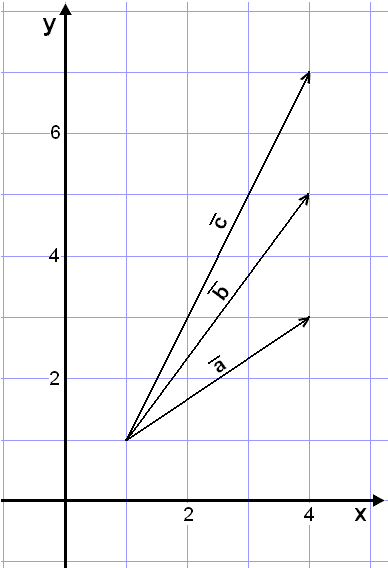
Find the components of the vector
parallel
to
and
.
The following relation holds:
=
r×
+ t×
We need to find the numbers r and t.
Putting in the coordinates we get:
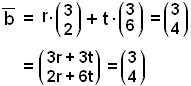
This leads to two equations with two unknowns r and t.
The
x-coordinates give the equation 3r
+ 3t
= 3 or r +
t
= 1
and the y-coordinates give 2r
+ 6t
= 4 or
r
+ 3t
= 2
Solving these equations, for example by subtracting the x equation from the y equation gives:
r + 3t = 2
−r − t = −1
2t = 1
t = ½ og r = ½
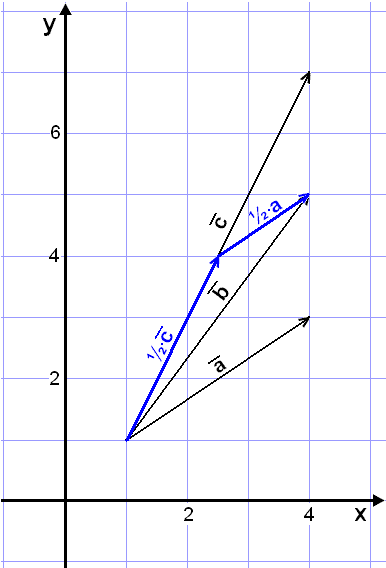
The solution is therefore
= ½×
+ ½×
as can be seen in the diagram.
Try Quiz
2
on Vectors.
Remember to use the checklist to keep track of your work.
and 
