© 2008 Rasmus ehf and Jóhann Ísak
Vectors
|
© 2008 Rasmus ehf and Jóhann Ísak |
Vectors |
|
Vectors in the coordinate system
The
point A has coordinates (2, 2) and the point B coordinates (6, 5) (see diagram).
The coordinates of the vector
are
We
can use the formula for the distance between two points to find the distance
between A and B, that is the length of the vector
(see Pythagoras Rule in lesson 2). The formula is as follows:
Putting the given coordinates into the formula we get:
We see that the numbers under the square root are simply the coordinates of the vector. This is, of course, because the length of the vector is simply the hypotenuse in a right angled triangle with shorter sides 3 and 4.
The formula for the length of a vector that starts in the point
A = (x1, y1) and ends in B = (x2,
y2) is:
|
|
If the coordinates of the vector are
then we have the following rule:
|
|
Find the vector
which is parallel to
and which has a length of 2 units
(see
the diagram).
The two triangles in the diagram are similar and therefore the corresponding
sides are in the same ratio.
|
|
= t∙||.
The number t is the ratio between corresponding sides. The ratio is 
.
We can find the coordinates of as
follows:
If
the vectors
and
are
parallel then there exists a number t such that:
|
|
Which of the following vectors are parallel
and
.
If
vectors
and
are
parallel then there exists a number t such that =
t∙.
If the vectors
and
are
parallel there exists a number r such that
=
r∙.
We can find numbers t and r by using the x-coordinates and then check to see whether the same values are found when we use the y-coordinates.
= t∙
3 = t∙13½ gives t = 3/13½ =2/9
4 = t∙18 also gives t = 4/18 = 2/9
The
vectors
and
are
parallel.
= r∙
3 = r∙6 gives r = ½
4 = r∙9 gives r = 4/9
The
vectors
and
are
not parallel
(This means that
and
are
not parallel either).
The vector in the diagram has coordinates
.
The
vector starts in the point (0, 0) and ends in (3, 2) so the coordinates of the
end point are the same as the coordinates of the vector itself. This is true of
all vectors that start in the origin of the coordinate system, that is in the
point (0, 0).
|
A vector that starts in the point (0, 0) has the same coordinates as it’s end point. This vector is called the position vector for A. |
Every point in the coordinate system can be represented by it’s position vector. The coordinates of a point and it’s position vector are the same. This can be very useful when looking at translations in the coordinate system.
The triangle shown in the diagram is to be translated by the vector
.
We use the position vectors of the vertex points (−3, 0),
(2, −2) and (3, 1) and add the vector
to each of them.
This gives us the new position vector of each of each vertex. The diagram below shows the translation.
We will now use position vectors to find the midpoint of the line segment AB if A = (1, 2) and B = (4, 3).
As usual the point O is the origin of the coordinate system. If M the midpoint of AB then:
=
+ ½∙
The vector
is
the position vector of the point M and therefore has the same coordinates as the
point M that we wish to calculate. The vector is
the position vector of A. To reach the midpoint M we need to add half of the
vector .
Draw a diagram to see this.
First we need to find the vector
.
Now we can find
.
=
+ ½∙
The coordinates of M are the same as those of the position vector
or (2½, 2½).
It‘s easy to find a formula that we can use to find the coordinates of the midpoint of a line segment AB.
|
From the diagram we can see that the midpoint M can be reached from two directions, from O via A to M and from O via B to M.
We can therefore write two vector equations for
Adding these two equations together we get |
 |
2
= + ½∙
+ 
- ½∙
We see that the position vector of the midpoint of the line segment is a kind of
average of the position vectors of the end points. We can therefore find the
coordinates of the midpoint by finding the average of the x coordinates and y
coordinates respectively.
This leads us to a rule we call The Midpoint Rule.
|
The midpoint M of the line segment AB is given by the rule:
Using coordinates the rule is:
|
The vertices of triangle ABC are A = (1, 2), B = (4, 3) and C = (3, 0).
Find the length of the line from A to the midpoint of the side BC (the median of triangle ABC ).
We begin by finding the midpoint of BC using the above rule.
We call the midpoint M and find its position vector
(see
diagram).
|
|
 |
Therefore M, the midpoint of BC has coordinates
M = (3½, 1½).
Next we find the coordinates of the vector
.
Finally we can find the length of the vector as
required.
≈ 2.55
|
The three medians of a triangle all intersect in one point, called the centre of the triangle (labelled T in the diagram). If we know the coordinates of the vertices of the triangle we can find the coordinates of T with a simple formula. This formula is found in a similar way to the Midpoint Rule. We can reach T via all three vertices of the triangle, then we add the three vector expressions together. |
 |
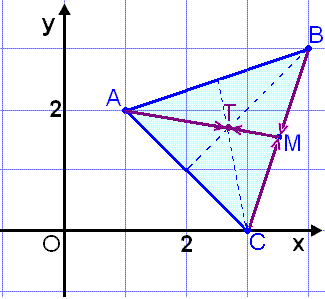In lesson 2 about triangles we saw that the medians all intersect in one
point dividing each other in the ratio 2:1, or 2/1. From this we know that
the length of vector
is twice that of 
and therefore
=
∙
and
=
−
∙.
Using this we can write three equations:
=
+
∙
=
+ ½∙
-
∙
=
- ½∙
- ∙
When we add them together ,
goes out and we get:
3
=
+ +
 |
To find the coordinates of T we take the average of the x and y coordinates of the vertices respectively. |
We therefore find the point of intersection, T, of the medians of a triangle by finding a kind of average of the position vectors of the vertices. This rule is therefore an extension of the Midpoint Rule.
|
Find the point of intersection, T, of the medians of the triangle ABC ( the centre ) given that A = (1, 2), B = (4, 3) and C = (3, 0) (see diagram).
|
 |
The centre T =
(2
,
1
).
Try Quiz
3
on Vectors.
Remember to use the checklist to keep track of your work.
