© 2008  Rasmus ehf  and Jóhann Ísak

Vectors

Lesson 4

Scalar product and perpendicular vectors

How can we find the angle between two vectors? The Cosine Rule looks promising as we can use it to find the angle between two sides of a triangle. (See lesson 3 on triangles). We can make a triangle out of the two vectors   and , and a third vector  −  (see lesson 1 on vectors 1). Look at the diagram below.

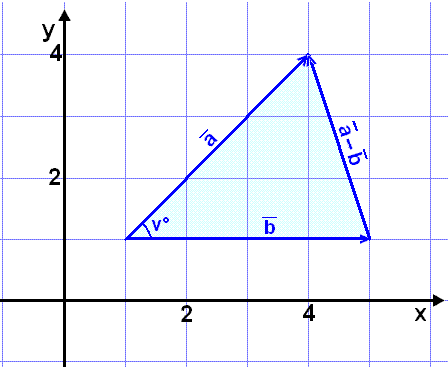
In this example it’s easy to find the vectors by counting the squares, but we will use the general form for any vector:

The Cosine Rule is as follows:

    c ² = a ² + b ² − 2∙b∙a∙cos C

The sides of the triangle have lengths ||, || and | − |. If we label the triangle so that side a = ||, b = || and c = | − | and label angle  C as v° we get:

| - |² = ||² + ||² - 2∙||∙ ||∙cos v°

Now we can use the distance formula to find the length of the vectors. We can leave out the square root as we are squaring the lengths.

    (x_a − x_b)² + (y_a − y_b)² = x_a² + y_a² + x_b² + y_b² − 2∙||∙ ||∙cos v° 

If we simplify the left hand side by multiplying out the brackets it becomes:

   x_a² − 2x_ax_b + x_b² + y_a² − 2y_ay_b + y_b²

Putting this in the formula we see that all the squared terms cancel out and we are left with the equation

   − 2x_ax_b − 2y_ay_b = − 2∙||∙ ||∙cos v° 

Dividing through by −2 we get the following important formula:  

Each side of this equation is called the Scalar Product of two vectors. In other words:

The  scalar product of  and  = x_ax_b + y_ay_b and
the scalar product of  and  = ||||cos v°

The symbol for scalar product is a point similar to the symbol sometimes used for multiplication. Its very important to distinguish between the two. A dot written between two vectors is always the scalar product. In fact it is often called the Dot Product.  Using this notation we can write:

∙ = x_ax_b + y_ay_b  and  ∙ = ||∙ ||∙cos v° 

Example 1

Write  the scalar product of the vectors  and  in the following diagram in two different ways.

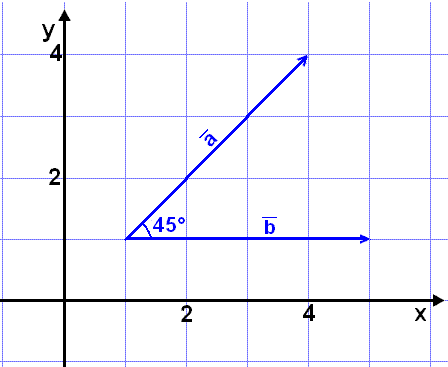
We can read the coordinates of the vectors directly from the diagram. We can also see the length of the vector  but we need to calculate the length of vector .

Using coordinates to find the scalar product:

Using the other definition of scalar product with vector lengths and cosine we get:

|| =

|| = 4

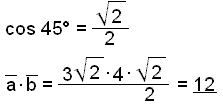
Now we will answer the question we set out with and see how we can find the angle between two vectors.

To do this we use both forms of the scalar product.

    x_ax_b + y_ay_b = ||∙ ||∙cos v° 

Dividing through by |||| we get the following formula:
 

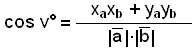If we use the distance formula to find the lengths this becomes:

Example 2

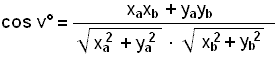Find the angles between the vectors

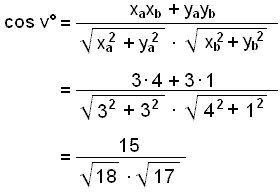
               ≈ 0.8575

           v° ≈ cos⁻¹ 0.8575 ≈ 31°

Example 3

Find a vector that is the same length as and perpendicular to .

We call this vector and write the formula for the scalar product of  and .

   x_ax_b + y_ay_b = ||∙ ||∙cos 90° 

But cos 90° = 0 so we get the following result:

   x + 2y = 0

We also know that ||²  = x² + y² = 5.

Solving these two equations together we get , x + 2y = 0 and x² + y² = 5.

    x = −2y  and  x² = 5 − y²

   x² = 4y² = 5 − y²

 5y² = 5

   y² = 1

    y = ±1

If y = 1 then  x = −2 and if y = −1 then x = 2.

This means we have two possibilities

Drawing the diagram we see these two outcomes.

Generalising the above results we see that we can find two vectors that are perpendicular to each other and of the same length by switching round the x and y coordinates and changing the sign on one of the coordinates.

This is because the angle between perpendicular vectors is 90° and  cos 90º = 0

The converse of this rule is also true.

Example 4

Triangle ABC has vertices A = (–3, –4), B = (17, –12) and  C = (5, 16). Find the angles of the triangle.

First we find vectors that represent the sides.

We don’t need to do any more work as the vectors  and  are obviously perpendicular and equal in length. The triangle is therefore a right angled isosceles triangle with angle A = 90º, B = 45º and C = 45º.

Example 5

Triangle ABC has vertices A = (–3, –3), B = (21, 7) and  C = (4, 14).

a)  Find the angle A

     First find the vectors and .

      Now find their lengths.

       Finally we find the angle A, between and .

Multiply by Ö2 above and below the fraction line

b)  Find the height from C onto the side AB.

         sin A = h/||

         h = || · sin A

            = 13·Ö2·Ö2/2

            = 13

c)   Find the vector  from C to AB, perpendicular to AB.

      The vector  is perpendicular to  and twice as long. We can therefore find  by turning   through 90º and dividing the coordinates by 2.

Try Quiz 4 on Vectors.
Remember to use the checklist to keep track of your work.