© 2009 Rasmus ehf & Jóhann Ísak
|
© 2009 Rasmus ehf & Jóhann Ísak |
Derivatives |
|
Derivatives of exponential and trig functions
 |
We're going
to use the CASIO-calculator to find some values of functions of the type f(x) = ax
where a is a constant and x is the variable. We will do this by fixing the value of x and looking at values of f(x) and f´(x) as a changes from 2 to 3. We can choose any value for x, for example x = 2. Choose the RUN menu and then the button labled OPTN next to the SHIFT-button. Next choose CALC with F4 and then d/dx withF2. Finally put in a komma and then the x value 2. |
|
|
 |
|
 |
||
The results are shown in the table below
|
a |
a2 |
f '(2) |
|
2.0 |
4.0 | 2.8 |
|
2.1 |
4.4 | 3.3 |
| 2.2 | 4.8 | 3.8 |
| 2.3 | 5.3 | 4.4 |
| 2.4 | 5.8 | 5.0 |
| 2.5 | 6.3 | 5.7 |
| 2.6 | 6.8 | 6.5 |
| 2.7 | 7.3 | 7.2 |
| 2.8 | 7.8 | 8.1 |
| 2.9 | 8.4 | 9.0 |
| 3.0 | 9.0 | 9.9 |
The value of
a2
goes from 4 when a = 2 up to 9 when a = 3. The derivative goes from 2.8
up to 9.9 (both numbers are approximate). Both columns of numbers change
continuously so somewhere, not far from 2.7, the function and it's derivative
take the same value.
We will see this happening in exactly the same place whatever value we choose
for a.
If we choose a = 2.718282 we get the same value in both columns up to the
sixth decimal place (7.3890570 and 7.3890575). You should recognise this number
from the lesson on natural logarithms. It's the number e.
The number e is an irrational number and therefore we can
only give an approximate value for e, e
![]() 2.718282 . The function f(x) = ex
remains unchanged when we differentiate it, that is f(x) = f´(x) = ex
2.718282 . The function f(x) = ex
remains unchanged when we differentiate it, that is f(x) = f´(x) = ex
|
The derivative of the function f(x) = ex is f´(x) = ex |
In lesson 5 you will see a rule called the Chain Rule. One of the results of this rule is that if x is multiplied by a constant number then the differentiated function is also multiplied by that constant . For example if we differentiate f(x) = e2x we get f´(x) = 2e2x .
In general, if k is a constant and f(x) = ekx then f´(x) = kekx .
Using this fact we can find the derivative of the function f(x) = ax. Using the log rules x = eln x and ln ax = x·ln a we can rewrite f(x) as
f(x) = ax = ex·ln a
a is a constant, so ln a is also a constant like the k in the above rule. So we can differentiate the function by writing it in the form ex·ln a.
f´(x) = (ex·ln a)´ = (ln a)·ex·ln a = (ln a)·ax
|
The derivative of f(x) = ax is (ln a)·ax |
Example 1
Find the derivative of f(x) = ex·ax.
Using the multiplication rule (uv)´= u´v + uv´ with u = ex and v = ax gives us u´ = ex and v´ = (ln a)·ax. Putting these values into the formula we get
f´(x) = (uv)´= u´v + uv´
= ex·ax + ex·(ln a)·ax take exax outside a bracket .
= exax(1 + ln a)
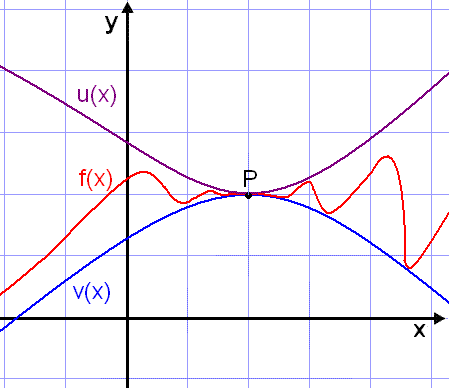
Now we consider a rule
often referred to as the sandwich rule. This is a method we can use to solve
difficult limit problems. If we are unable to find the limit of a function f(x)
in a particular point P we can try to find a function u(x) that has the same
value as f(x) in the point P but is greater than f(x) in the neighbourhood of P.
In the same way we find a function v(x) that takes the same value as f(x)
in the point P but is less than f(x) in the neighbourhood of P. In this way we
sandwich f(x) in between
u(x) and v(x) . If these two functions u(x) and v(x) have the same limit in
point P then f(x) must also have this limit. This is demonstrated in the diagram
below.
Now we will use the
sandwich rule to find
![]() .
The problem is
that if we put 0 in for the x then we get 0/0 which we have a problem
evaluating.
.
The problem is
that if we put 0 in for the x then we get 0/0 which we have a problem
evaluating.
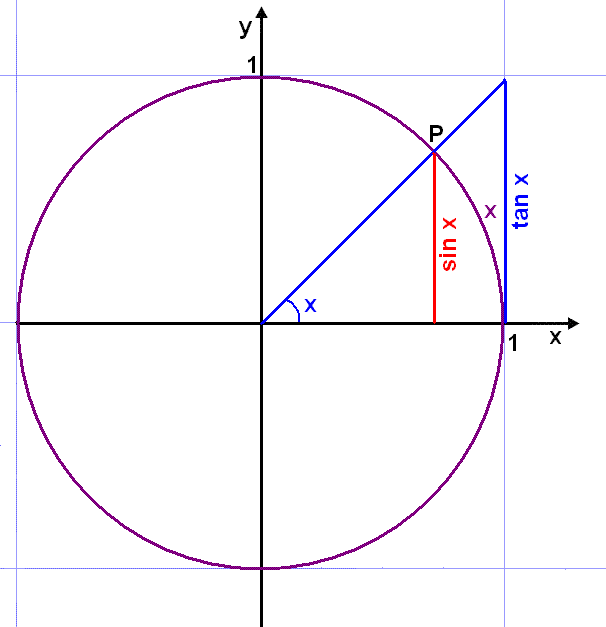
The above diagram shows the unit circle. We have drawn the angle x. If x is measured in radians then the length of the arc between the point (1, 0) on the x axis and the point P is also x . The vertical red line has length sin x and is obviously less than the arc x which is again less than tan x . We can write the following inequality:
sin
x
![]() x
x
![]() tan x
tan x
Remember tan x is defined as
![]() so we get
so we get
![]()
Dividing all through by sin x and cancelling
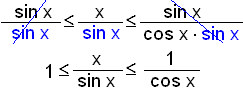
Inverting all the fractions and reversing the inequality symbols gives us
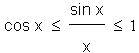
We have succeeded in
sandwiching
the fraction
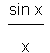 between
1 and
cos x
between
1 and
cos x
which both have the limit 1 as x tends to 0 .
This gives us the rule
![]() = cos 0 = 1
= cos 0 = 1
We use this rule in the following examples .
Consider the limit
![]() .
.
In this case we don't need to use the sandwich rule, instead we use (a + b)(a – b) = a2 – b2 first multiplying the fraction all through by (cos x + 1)
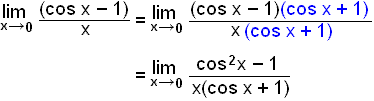
Remember Pythagoras's rule for cos and sin, cos2x + sin2x = 1 which can be rewritten as –sin2x = cos2x –1.
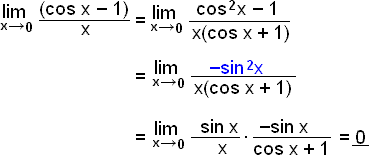 |
We continue the example as follows: |
The first fraction has the limit 1 from the above rule and the second fraction is 0 because sin 0 = 0. This gives the result
Example 2
We can now set about finding the derivative of sin x.
|
(sin x)' = |
|
Using one of the addition rule for trig functions sin(u + v) = sin u cos v + cos u sin v and putting it into the above expression we get:

In the last line of the proof we used the results of the two limit rules that we proved earlier in this lesson. We get the very satisfactory result that the derivative of sin x is cos x.
A similar method gives the result that the derivative of cos x is – sin x.
|
sin´x = cos x cos´x = - sin x |
Example 3
Find the derivative of f(x) = tan x.
Remember that ![]() and use the rule for the derivative of quotients
and use the rule for the derivative of quotients
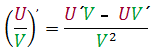 .
.
In this case u = sin x and u´ = cos x, v = cos x and v´= – sin x. Putting these values into the rule we get
 |
Here we use the rule |
Practise these methods and then
take test 4 on derivatives.
ps. Remember your check list.