© 2009 Rasmus ehf and Jóhann Ísak
|
© 2009 Rasmus ehf and Jóhann Ísak |
Integration |
|
We have seen how derivatives can be used to find the gradient of tangents to a graph. The process of finding derivatives is called differentiation.
Conversely, the process of finding a function if we know it's derivative is called integration.
If f(x) is the derivative of a function F(x) then F(x) is called the integral of f(x). In other words F(x) is a function such that F´(x) = f(x).
A rocket is fired
vertically
and reaches a height of 130 m before falling back to earth.
Measurements show that the velocity of the rocket can be given by the formula
f(t) = 50 – 10t where f is the speed of the rocket after t
seconds.
When we were discussing
differentiation we noted that the derivative of the position function with
respect to time gives the velocity function. In this case we know the
velocity function and need to work backwards, that is integrate, to find
the position function or height. In other words we need to find a function F(t) such
that
F´(t) = 50 –
10t = f(t).
We know that if we differentiate 50t we get 50 (t´ = 1). We also know that when we differentiate a power, we multiply by the power index and then decrease the index by 1 ( (xn )' = nxn-1). The inverses process , integration, must increase the power by 1 and divide by the new power. This gives us the following result
F(t) = 50t –10t2/2 = 50t – 5t2
When a function is differentiated all constant values disappear so when we
integrate we have to add in an inknown constant that we call C (C´ = 0). The
final result of integration is therefore F(t) = 50t – 5t2 + C.
We can find the value of C by using the information given.
This shows us that C = 0.
The rocket slows down as it rises and reaches it's maximum height at 130 m . There the speed must be zero and we get:
f(t) = F´(t) = 50 – 10t = 0
10t = 50
t = 5
This tells us that the rocket reaches it's maximum height of 300m after 5 seconds. Putting this information into the equation for F, the height, we get
F(5) = 50·5 – 5·52 + C = 130
250 – 125 + C = 130
C = 130 – 125 = 5
and therefore F(t) = 50t – 5t2 + 5
From this we can see that when t = 0 then F = 5, which tells us that the rocket was fired from a height of 5 m .
Now we will do some examples to show how to find the integral of a polynomial function.
1) First consider the function f(x) = x.
The integral must be a second degree function because we know that when we
differentiate a second degree function the index decreases by one and we get a
first degree which is what we want. But when we differentiate x2
we get 2x, so we have to divide by 2 if we want just x. We also need to remember
that constant numbers disappear when we differentiate so we need to put them
back in when we integrate. Our final solution will therefore be
F(x) = x2/2 + C
Let's test our solution by differentiating:
F´(x) = f(x) = 2x/2 + 0 = x
which fits.
2) Find the integral of f(x) = x3.
We raise the power by 1, to 4, divide by the new power, 4, and then add the constant C.
F(x) = x4/4 + C
Testing the solution we get
F´(x) = f(x) = 4x3/4 + 0 = x3
3) Find the integral of f(x) = xn.
We raise the power by 1, divide by the new power and then add a constant, C.
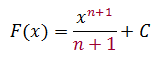
Now test the result:
F´(x) = f(x) = (n+1)xn+1–1/(n+1) + 0 = xn
which fits.
Find the integral function of f(x) = 3x2 – 2x + 1 that goes through the point (1, 1).
F(x) = 3x3/3 – 2x2/2 + x + C = x3 – x2 + x + C
First check by differentiation.
F´(x) = 3x2 – 2x + 1 + 0
This fits so now we can set about finding the constant C such that the graph of the function goes through the point (1, 1). This means that F(1) must be equal to 1 so we get
F(1) = 13 – 12 + 1 + C = 1 + C
The only way for F(1) = 1 is if C = 0, so the function we are looking for is
F(x) = x3 – x2 + x
Find the integrals of the functions f(x) = ex and g(x) = e2x that go through the point (0, 0).
Integrating the function f(x) = ex gives us F(x) = ex + C,
which can easily be checked by differentiating. We can find the constant C by
using the information that
F(0) = 0
F(0) = 0 = e0 + C = 1 + C
This gives us the value –1 for C and the final result
F(x) = ex – 1
The function g(x) = e2x must have an integral of the form e2x. Differentiating e2x gives 2e2x because, by the chain rule, we have to multiply by the derivative of the inner function which is 2x. So, if we multiply by 2 when differentiating we must divide by 2 when integrating, giving us
G(x) = e2x/2 + C
( Checking G´(x) = g(x) = 2e2x/2 + 0 = e2x
)
We can write the following rule:
The integral of the function
f(x) = ekx
is
![]() .
.
Now we can find the constant C as before:
G(0) = 0 = e0/2 + C = ½ + C
Which means that C = –½ giving the final solution
G(x) = ½e2x – ½
Find the integral of f(x) = ax.
If we differentiate f(x) = ax we get f '(x) = ax ln a. So, as ln a is a constant that multiplies ax when we differentiate, we must divide by the same constant when we integrate. So if F(x) is the integral function of f(x) = ax then we get that
![]()
Integrate the trig functions f(x) = sin x, g(x) = cos x and h(x) = cos 2x.
We have previously proved that
f´(x) = cos x
and g´(x) = –sin x so the integral must also be an exchange of the
functions. If we guess that cos x is the integral of
f(x) = sin x and differentiate to check we get an extra minus sign. This means
that the integral of sin x must be –cos x. On the other hand if we
test whether sin x is the integral of cos x we get the correct answer. The
integrals are therefore as follows:
F(x) = –cos x + C
G(x) = sin x + C
Now look at the third function in the example h(x) = cos 2x. If we
guess that the integral is H(x) = sin 2x and differentiate to test
our answer we get
H'
(x)
= 2·cos 2x ( the chain rule is used ) which is double the answer
that we want. So again, when we integrate we need to divide by this constant
factor, 2 giving the solution
H(x) = ½·sin 2x + C
Now we'll integrate some functions involving roots. We do this by changing the roots to powers and using the rule from Example 3 where we found that the integral of the function f(x) = xn is
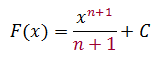
1) Find the integral of f(x) = .
Rewriting as a power gives
![]() , now we use the
above rule and get
, now we use the
above rule and get
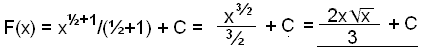
2)
Find the integral of
![]() .
.
Rewriting as a power,
![]() which means that
which means that
![]()
3)
Find the integral of ![]() .
.
Rewriting as a power
![]() .
.
![]()
Find the integral of f(x) = 1/x.
It's natural to first try changing to a power and rewriting as f(x) = x–1
We soon see that this doesn't work because it gives F(x) = x–1+1/(–1+1) = x0/0 which is undefined.
We need to remember the rule: (ln x)´ = 1/x, which tells us that the integral of f(x) = 1/x must be ln x.
We also need to remember that ln x only exists for values x > 0, so the integral of f(x) = 1/x is
F(x) = ln ІxІ + C
The following table of integrals summarises the above results:
|
Function |
Integral |
|
0 |
C |
|
1 |
x + C |
|
x |
½x2 + C |
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
–cos x + C |
|
sin ax |
|
|
cos x |
sin x + C |
|
cos ax |
|
Practice these methods then take
test 1 on integration.
Remember the check list!!