© 2010  Rasmus ehf    og Jóhann Ísak Pétursson

Integration

Lesson 5

Integration using partial fractions

We know that the integral function of  f(x) = 1/x is F(x) = ln lxl.

Let's check whether this applies to functions of the type f(x) = 1/n(x) where n(x) is of the form ax + b (a and b are constants).

First check whether = ln lx + 1l + C .

Do this by differentiating the integral function:

   (ln lx + 1l + C)´ =  .

This is correct.

Now we will try the same with  . 

We make a guess that the integral is  2·ln l3x + 4l + C and then differentiate to check.

   (2·ln l3x + 4l + C)´ = .

In this case we have to use the Chain Rule to differentiate which gives us an extra 3 when we multiply by the derivative of the inner function. This means that the answer we guessed at is incorrect. We can put things right by dividing by the extra 3.  The correct integral function is therefore ⅓·2·ln l3x + 4l + C. Generalising gives us the following rule:

Now we move on to look at functions with a quadratic in the denominator.

Before we do this let's revise some fractions.

Simplify

The common denominator is  6 so we get

2 divides 3 times into 6  so we multiply the first fraction above and below the dividing line by 3. In the same way the second fraction has to be multiplied by 2.

Here's another example using letters instead of numbers: 

The common denominator is  xy so we lengthen the first fraction by y and the second by x.

Now a slightly more difficult example.

The common denominator is  (x + 2)(x + 1) so we have to lengthen the first term by (x + 1) and the second by (x + 2).

Now let's work backwards and try to split this example back into the two original parts.

First factorise the denominator

  x² + 3x + 2 = (x + 2)(x + 1)

This gives us the denominators but we don't know what the numerators are going to be. We call them a and b so that the following must be true:

The problem is solved if we can find a and b.

To do this we put the right hand side of the equation back together:

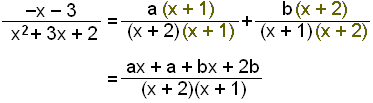
This type of equation is called an identity because the left and right hand side are always the same whatever value x takes. There are two main ways of solving these types of problems.

One way is to compare both sides of the equation. The x's on both sides have to be equal and the constant terms have also to be equal.

This means that  ax + bx = −x  and therefore a + b = −1 and also  a + 2b = −3

We get the following pair of simultaneous equations:

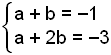
Solving these gives  b = −2 and  a = 1 which checks out with the original example

The second method of solving this identity is by choosing values of x. If we look at the numerators on both sides of the identity we see that

−x − 3 = a (x + 1 ) + b ( x + 2 ). 

As the identity is true for all values of x we can choose any x value.

If we choose x = − 1 we get −(−1) −3 = a(−1 +1 ) + b ( −1 + 2 )

The term in a falls out  and we immediately see that  b = − 2.   ( 1 − 3 = b ( 1) )

Choosing x = − 2 means the b term drops out and we get a = 1.

This second method means that we don't have to solve any simultaneous equations.

Example 1 

= 2∙ln lx + 1l + C

Example 2

= ½∙2∙ ln l2x + 1l + C = ln l2x + 1l + C

Example 3

 We begin by finding the partial fractions  .

        x² – 1 = (x + 1)(x – 1)

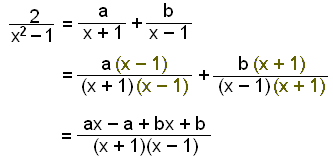
     and finding  a and b.

     There are no terms in x on the left  so ax + bx must be 0.

     The constant term on the left is  2  and on the right is  –a + b .

     This gives us the pair of simultaneous equations:

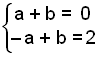
    which can easily be solved.

    For example adding the two equations together gives us 2b = 2 and therefore b = 1.

    Putting the value b = 1  into either of the equations gives a = −1.

    Now we can rewrite the function as the sum of two fractions with a first degree polynomial in the denominator and integrate.

Example 4

    Begin by factorising the denominator

       x² + 3x + 2 = (x + 1)(x + 2)

     Next split into partial fractions.

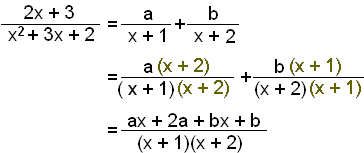
    Comparing the terms in x on both sides of the equation gives ax + bx = 2x or a + b = 2.

    Comparing the constants gives 2a + b = 3.

    Now solve the pair of equations

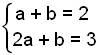
    Subtracting the first from the second gives  a = 1 and putting this into one of the equations gives  b = 1.

    Now we can integrate.

Example 5

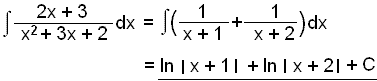
  Factorise:  x² + 3x = x(x + 3)

    Find the partial fractions

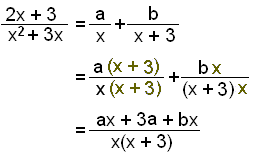
    Comparing constant terms:  3a = 3 and a = 1.

    Comparing terms in x: ax + bx = 2x , giving us   a + b = 2 and therefore b = 1.

    Integrating:

Example 6

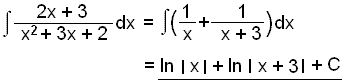
   Factorising: x³ – 5x² + 4x = x(x² – 5x + 4) = x(x – 1)(x – 4)

    Partial fractions:

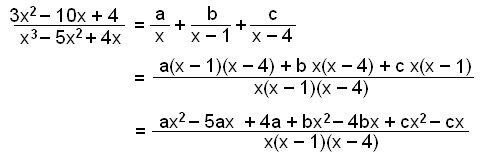
    Comparing terms in x² : ax² + bx² + cx² = 3x² which means that  a + b + c = 3.

     Comparing terms inx:  −5ax – 4bx – cx = −10x gives us the equation 5a + 4b + c = 10.

    Finally comparing constant terms 4a = 4 so that a = 1.

     Putting this value for a into the other equations:

    1 + b + c = 3 or b + c = 2 

     5 + 4b + c = 10 or 4b + c = 5.

     Subtracting the equation b + c = 2 from 4b + c = 5

     gives us 3b = 3 or b = 1.

     Putting in the b value: 1 + c = 2 or c = 1.

    Integration:

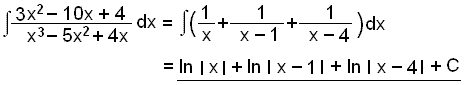
Practise these methods then take  test 5 on integration.

Remember the check list!!