© 2008 Rasmus ehf and Jσhann Νsak Pιtursson
|
© 2008 Rasmus ehf and Jσhann Νsak Pιtursson |
Sequences and Series |
|
A sequence of numbers can follow a given rule or be completely random. Sequences that follow a given rule or pattern, such as the repayment of bank loans are particularly interesting mathematically. Each term in a sequence is given a number from 1 to n, the number defining the position of the term in the sequence. In mathematics the terms are commonly written using small letters with a subscript to show their position in the sequence. The sequence of numbers in the five times table could be written as follows:
a1 = 5
a2 = 10
a3 = 15
e.t.c.
The following table gives a few examples of sequences that follow given rules. See if you can spot the rule.
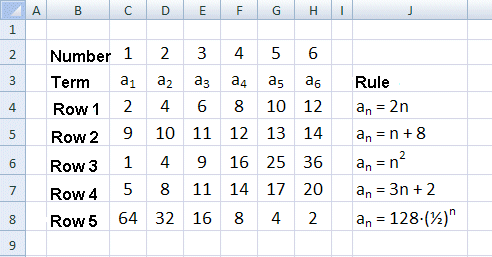
All these sequences have terms that can be written as functions of n, f(n) where n is a whole positive number.
Other sequences exist that follow a given rule but which can't be written as functions of n. A well known example of this is what is called the Fibonacci sequence. The first two numbers in this sequence are 1 and 1, the rest are found by adding together the two previous numbers in the sequence giving the following:
1, 1, 2, 3, 5, 8, 13, 21 e.t.c
In this case the rule is a1 = 1, a2 = 1 and an = an−1 + an−2 for n > 2
To show that a sequence carries on infinitely we write a row of dots.
1, 1, 2, 3, 5, 8, 13, 21, . . . . . .
This is a method that will be used for all sequences of infinitely many terms. Dots are also used in the middle of a sequence of finite terms once the rule is obvious.
For example the sequence of whole numbers from 1 up to 10 is written as
1, 2, 3, . . . ,10
Now we will look at a particular type of sequence where the difference between consecutive terms is always the same. For example the sequence
2, 5, 8, 11, 14, . . . .
where the first term is 2 (a1 = 2) and the rest of the terms are found by adding ther number 3 to the previous term. In other words the difference between consecutive terms is always 3.
This type of sequence is called an Arithmetic sequence or Arithmetic Progression, AP for short.
Let's find a rule for calculating any term, say the tenth term.
a1 = 2
a2 = 2 + 3 = 5
a3 = 2 + 3∙2 = 8
a4 = 2 + 3∙3 = 11
We see that we can find any term by
multiplying together 3 and a number one less than the number of the term, then
adding 2.
So that the tenth term would be 3 times 9 (10 - 1) plus 2.
a10 = 2 + 9∙3 = 29
If we use d for the difference we get the following rule for an AP.
|
an = a1 + (n 1)∙d |
The first two terms in an AP are
a1 = 1 and a2 = 5
Find the twentieth term a20
The difference d = a2 − a1 = 5 1 = 4
We find the 20 term using the formula.
a20 = a1 + (n 1)∙d
= 1 + (20 1)∙4
= 1 + 19∙4 = 77
Find a formula f(n) for the n th term in example 1.
f(n) = a1 + (n 1)∙d
= 1 + (n 1)∙4
= 1 + 4n 4
= 4n − 3
In an AP we have the following information:
a20 = 82 and a21 = 85
Find a1 and a formula for the n th term.
The difference between two consecutive terms is d where
d = a21 a20 = 85 82 = 3
We put this into the formula for a20 to find the value of the first term.
a20 = a1 + (n 1)∙d
= a1 + (20 1)∙3
= a1 + 19∙3 = a1 + 57
85 = a1 + 57
85 57 = a1
a1 = 28
Now we can put these values into the rule for an AP to find a formula for an
an = a1 + (n 1)∙d
f(n) = an = 28 + (n 1)∙3
= 28 + 3n 3
= 3n + 25
In an AP we are given that a4 = 8 and a10 = 128. Find the first five terms.
The difference between a4 and a10 must be six times the difference d, between consecutive terms (10 4 = 6).
6d = 128 8 = 120
d = 120/6 = 20
Putting this into the rule for an we get
an = a1 + (n 1)∙d
a4 = a1 + (4 1)∙20
8 = a1 + 3∙20
a1 = 8 60 = −52
Now we can find the first five terms by adding 20 to the previous term.
a2 = −52 + 20 = −32
a3 = −32 + 20 = −12
a4 = −12 + 20 = 8
a5 = 8 + 20 = 28
There are 5,500 people living in a small town. From previous years we can estimate that the population increases at the rate of 450 a year. When will the population reach 10.000?
Using the equation an = a1 + (n 1)
with an = 10,000, a1 = 5,500 and d = 450 we get
10,000 = 5,500 + (n 1)∙450
Solving for n.
10,000 5,500 = (n 1)∙450
4,500 = (n 1)∙450
4,500/450 = n 1
10 = n 1
n = 11 years
Practise these methods then try
Quiz 1 on Sequences and Series
Remember to use the checklist to keep track of your work.