© 2008  Rasmus ehf  and Jóhann Ísak Pétursson

Sequences and Series

Lesson 4

Geometric series

When the terms of a geometric sequence ( GP) are added together we get what is called a geometric series. We can easily find a rule for the sum of n tems , Sn  of such a series.

Sn = a1 + a1∙k + a1∙k2 + a1∙k3 + ∙ ∙ ∙ ∙ ∙ + a1∙kn−2 + a1∙kn−1

Multiply all through by the common ratio k ( this raises the power of each term by 1) .

Sn∙k = a1∙k + a1∙k2 + a1∙k3 + ∙ ∙ ∙ ∙ ∙ + a1∙kn−1 + a1∙kn

Subracting the original expression from this

All but the first and last terms cancel out and we can solve the resulting equation for  Sn:

   Sn ∙ k – Sn = a1 ∙ kn – a1

   Sn ∙ (k – 1) = a1 ∙ (kn – 1)

Dividing through by  (k – 1)  gives the following rule:

Example 1 

Find the sum of the first ten terms in the following geometric series: 

   1 + 2 + 4 + 8 + 16 + ∙ ∙ ∙ ∙ ∙

We have n = 10, k = 2 and  a1 = 1. That's all we need to know to be able to use the rule.

   

          = 1024 −1 =1023

Most series are easy to solve using EXCEL.                   

1) 2) 3) 4)

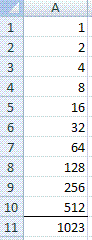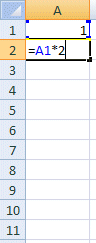
1)  Begin by putting the first term in cell A1. Write the formula =A1*2 in cell A2. This doubles the number in the cell above.

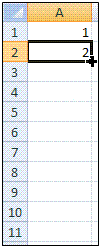
2)  Copy the formula in A2 down to  A10. The sequence should now be in A1 to A10.

3)  In cell A11 we put the formula  =SUM(A1:A10) by using the  ∑ symbol on the tool bar.

4)  The result should check out with the previous calculations.

Example 2

Find the sum of the series 1 + 3 + 9 + ∙ ∙ ∙ ∙ ∙ ∙177147. The terms are a GP with the ratio k = 3 and  a1 = 1

The first thing we have to do is to find the number of terms, n.
                an = a1∙kn−1

       177147 = 1∙3n−1

   ln 177147 = ln 3n−1

   ln 177147 = (n – 1) ln 3

   ln 177147/ln 3 = n – 1

   n = 1 + ln 177147/ln 3 = 12

Now we can use the sum formula.

   

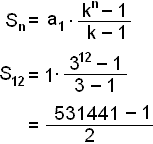
          = 265,720

 

Example 3

Find the sum of the first 7 terms of the geometric series with  a3 = 810,000 and a6 = 590,490.

We begin by finding the ratio k.

we can see that  a6/a3 =  k3 , where k is the ratio.

   k3 = 590,490/810,000 = 0.729          

   = 0.9   

Now we need to find the first term a1. We can do this by dividing  a3 by  k2.

   a1 = 810,000/0.92 = 1,000,000

Now we have all the information needed to use the formula:

     

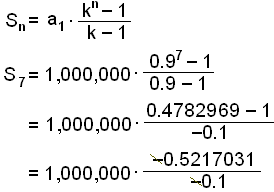
         = 5,217,031

In the above example the terms decrease as n increases. This is because the ratio, k, is between  -1 and 1. We have previously seen that GPs where the terms tend to zero as n increases to infinity are said to be convergent. Geometric series made up of terms that converge to zero as n tends to infinity are called Convergent series.

Geometic series are convergent if  −1 < k < 1.

Imagine someone taking part in a 100m race. First he has to run half the distance that's 50 m. Next he runs half of the distance that is left, that is 25 m , then 12.5m  and so on. In this way we can imagine the distance divided into smaller and smaller parts. Eventually, after adding together infinitely many parts, the runner has covered the whole distance.  Writing this mathematically we get:

   100 = 50 + 25 + 12.5 + 6.25 + ∙ ∙ ∙ ∙ ∙ ∙ ∙

Now we will find a formula for adding together infinitely many terms of a Geometric Series.

First consider what happens to  kn when n tends to infinity. It's obvious that if the absolute value of the ratio k is less than 1   (|k| < 1) then kn tends to  0 as n tends to infinity.

  

Now we can look at the formula for the sum of n terms of a converent series.

When talking about the sum of an infinite series we use S instead of Sn . kn  tends to  0 so we get

Multiplying above and below by  −1 to get rid of the negative gives us the formula:

 

Example 4

Find the sum of the geometric series   1 + ½ + ¼ + ⅛ + ∙ ∙ ∙ ∙ ∙ ∙

The ratio k = ½ so we can use the formula.

   

 

Example 5

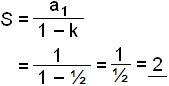
Find the sum of the geometric series

   1 − ½ + ¼ − ⅛ + ∙ ∙ ∙ ∙ ∙ ∙

In this case the terms alternate between + and – and the ratio k =  −½.

   

 

Example  6

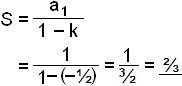
Find the value of the ratio k if the sum of the geometric series  1 + k + k2 + k3 + ∙ ∙ ∙ ∙ ∙ ∙ is 10.

This is a convergent geometric series so we use the formula.

Multiplying by  (1 – k) and solving the equation for k gives

     1 = 10(1 – k) = 10 – 10k

  10k = 10 – 1 = 9

      k = 9/10 = 0.9

Practise these methods then try  Quiz 4 on Sequences and Series  
Remember to use the checklist to keep track of your work.