1. Adding fractions with a common denominator

2. To add fractions that have different denominators, first change the fractions to equivalent fractions with the same denominator.  

Multiply the numerator and the denominator of a fraction by the same number to make the denominators the same

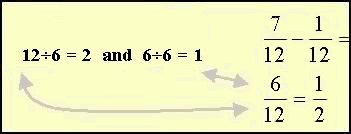
		You can always find a common denominator by multiplying the denominators of the fractions, even though the product may not be the lowest common denominator.
2×3 = 6  and  3×2 = 6		Here you see that when the denominators are multiplied you get a common denominator of 6.
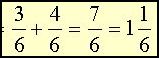		Now you can add the numerators and if necessary, change to a mixed number to get the answer.

3. Mixed numbers consist of whole numbers and fractions. To add mixed numbers with fractions that have different denominators, first find equivalent fractions that have the same denominator.  

		First find equivalent fractions that have the same denominator.
		Multiply the denominators to find a common denominator.
3×   3,6,9,12,15,18,21,24....		The lowest common denominator is the smallest number that can be divided by both 3 and 5, which is 15.
5×   5,10,15,20,25.....
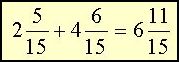
		Now add the numerators of the fractions and then the whole numbers.

4. Sometimes you may need to convert a mixed number. 

A whole number can be changed to a fraction. ( called borrowing) 
 

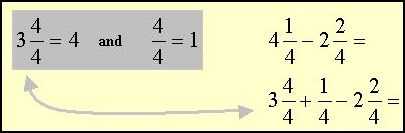
Add the numerators.
Notice  the denominator stays the same.

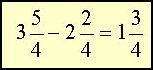
You know that 1 = 4÷4  (and 4 = 3+1)

5. Reduce fractions to their lowest terms. 

Give your answers in the lowest terms. 

If the larger fraction has a  minus sign (-) in front of it, the answer is negative. 

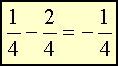
Try Quiz 1 on Common fractions (plus and minus).
You need to practice doing addition and subtraction of fractions with numbers until you can do the problems easily. The next lesson is about algebra fractions and it is important to understand the  basic ideas first.