Rasmus - Math, Ordered pairs equations and graphs, Lesson 3

Ordered pairs (coordinates )

Prin t

Lesson 3.

Equations and graphs

If you have two equations with two unknown values, there are at least three methods you can use to solve the equations.

Method 1: Plotting the lines in a coordinate system ( grid )

Look at the equations I: y = 2x + 1 and II: y = - x + 1.

Make a table of values for each equation.

y = 2x + 1
x	2x + 1	= y	x,y
-2	2·-2 + 1	-3	-2,-3
-1	2·-1 + 1	-1	-1,-1
0	2·0 + 1	1	0.1
1	2·1 + 1	3	1.3
2	2·2 + 1	5	2.5
3	2·3 + 1	7	3.7
4	2·4 + 1	9	4.9
5	2·5 + 1	11	5.11
6	2·6 + 1	13	6.13

y = -x + 1
x	-x + 1	= y	x,y
-2	-( -2) + 1	3	-2,+3
-1	-( -1) + 1	2	-1,+2
0	- 0 + 1	1	0.1
1	-(+ 1) + 1	0	..1,0
2	-(+ 2) + 1	-1	2,-1
3	-(+ 3) + 1	-2	3,-2
4	-(+ 4) + 1	-3	4,-3
5	-(+ 5) + 1	-4	5,-4
6	-(+ 6) + 1	-5	6,-5

Equation I

Equation II

If one or more common points can be found, the lines cross. Plot the lines on a grid.

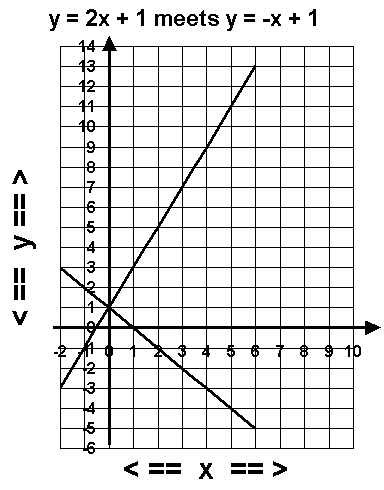
Here you see that the lines cross at the point (0,1). Notice that these lines have different gradients ( slopes ). Lines with different gradients always cross whereas different lines with the same gradient are parallel and therefore never cross.

Method 2: Adding the equations

Finding where the lines cross or intersect is the same as solving the equations. We can solve the equations by adding multiples of the equations together.

I: y = 2x +1

II: y = -x + 1

Begin by rearranging the equations:

I: -2x + y = + 1

II: x + y = 1

Multiply equation II by 2 to get 2(x + y = 1) or 2x + 2y = 2.

Add the equations:

I: -2x + y = 1

II: 2x + 2y = 2

0 + 3y = 3 therefore y = 1.

Substitute this value for y in Equation I to get the result -2x + 1 = 1.

Then move the unknown value to the right: 1 = 2x + 1.

Move the known values to the left side of the equation to get: +1 -1 = 2x or

0 = 2x. The result is x = 0.

This is the same result as was found by plotting the lines on a grid. The point (0, 1) is the only point that the two lines have in common.

Method 3: Substitution

Both conditions are true only when the lines cross. Therefore, we can say that y in Equation I and y in Equation II are the same at that point.

I: y = 2x +1

II: y = -x + 1

If we substitute the expression for y from Equation II into Equation I, we get the expression
-x + 1 = 2x + 1.

Move the known values to the left so that all the values are positive.

-1 + 1 = 2x + x or 0 = 3x The result is x = 0.

Substitute the value for x in Equation I to get y = 2·0 +1 = 0 + 1 = 1.

The lines cross at the point (0,1) as above.

It is important to understand these 3 methods if you plan on studying further maths.

Try Quiz 3 on Ordered pairs (equations and graphs).