Lesson 5

If you have understood the percentage explanations thus far, you should be able to calculate all the typical percentages needed in daily life and taught at lower secondary level.

The following percentage problems are more complicated and it is important to read the problems carefully in order to find the information necessary for their solutions. You can use the calculation methods explained previously.

Example:  

Increases or decreases

A jacket originally cost 60 euros but the price has been lowered by 25%.  What does the jacket cost now?

Find the reduction:   

 0.25 x 60 = 15

original price - reduction = new price
60 - 15 = 45

This method can also be used 

original price - reduction = new price

to find the new price in one step.

0.75 x 600 = 45

If the price of the jacket is increased by 25%, the increase is added to the original price:

original price + increase = new price
60 + 15 = 75

It can also be thought of as follows:

1.25 x 60 = 75

Example:

Comparison

Sean and Stephen both receive 5% pay increases next month. Will they receive the same amount of money? In order to answer this, we must know what their monthly wage was before the increase. Sean's wage was 1250 Euro and Stephen's wage was 1450 Euro.

Calculate the increase.

Sean's pay increase is:  0.05 × 1250  = 62.5 euros

Stephen's pay increase is:  0.05 × 1450  = 72.5 euros

You see that Sean and Stephen have different base wages. Therefore, the amount of Stephen's wage increase is greater than Sean's, even though the percent of the increase is the same. 

Example:  

If Sean tells Stephen that he has received a 5% pay increase and now makes 1365 Euro per month, we can calculate what his monthly wage was before the pay increase.

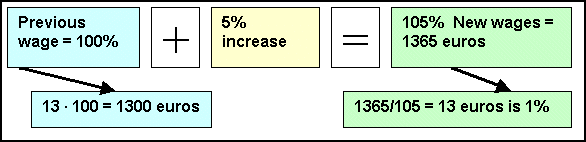
The problem can also be solved using the percentage equation: ·

Example:  

Annual increases

A new car cost 30,000 Euro at the end of the year 1998. The price has risen by 12% every year. How much does a new car cost 2 years later (at the end of the year 2000)?

Find the 12% increase:    0.12 × 30,000 = 3,600

New price:  30,000 + 3,600= 33,600  at the end of 1999.

Find the 12% increase on the new price:

0.12 × 33,600 = 4,032

The new price at the end of 2000:

33,600 + 4,032 = 37,632 euros

Try Quiz 5 in Percentages.