Lesson 3

Area of various planes (2 - dimensional figures)

    Parallelogram

If you know how to find the area of a square and a triangle , you can use that knowledge to find the area of other plane figures.

The basic shapes are  triangles, rectangles and circles. Most plane figures can be made from these basic shapes. In other words, most plane figures are combinations of these basic shapes.

 For example, a parallelogram can be broken down into a rectangle and 2 triangles. 
Planes can be broken down into basic shapes by drawing appropriate lines on the diagram.

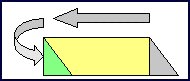
 It is also possible to move parts of a figure around to form other shapes. For example, you can change a parallelogram into a rectangle, as shown in the above diagram. The yellow and grey areas in the diagram form a parallelogram. If the grey triangle is moved to the left side of the parallelogram, it forms a rectangle (the green triangle plus the yellow figure). So you can calculate the area of a parallelogram by calculating the area of the rectangle.

   Trapezium

A trapezium is a four sided figure with two parallel sides.  The lines that have been added  show that a trapezium is made up of a rectangle and 2 triangles. The area can be found by adding together the area of the rectangle and the two triangles.

  Regular Hexagon

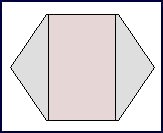
A  regular hexagon is a six sided figure, with all the sides of equal length. It can be divided into 2 triangles and a rectangle. The area can be found by adding together the area of the rectangle and the two triangles.

Practice these methods and then try Quiz 3 on Area. Remember to use the Checklist to keep track of your work.