© 2004  Rasmus ehf

Prime numbers

    Print

Prime numbers and divisibility

Lesson 1.

A prime number is a whole number greater than 1 that can only be divided by itself and 1. The smallest prime numbers are 2, 3, 5, 7, 11, 13, 17, 19 and 23.  The number 2 is the only even prime number. 

Example:  

7=1×7  The number 7 has only two factors: 1 and itself.  
11=1×11  The number 11 has only two factors: 1 and itself.  

Composite numbers:   A composite number has more than two factors. Composite numbers can be broken down into prime factors. 

Example:

6 = 2×3  2 and 3 are prime numbers.
20 = 2×2×5  2 and 5 are prime numbers.
35 = 5×7  5 and 7 are prime numbers.

Prime factors:    Find the prime factors of 30.

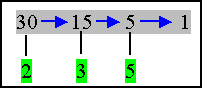30 = 2×3×5

The prime factors of 30 are the numbers 2, 3,  and 5. 
You can also find the prime factors of a whole number by drawing a factor tree. 
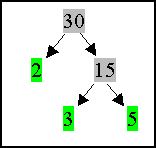30 = 2×3×5

 

Divisibility of numbers:        
You can use the Sieve of Eratosthenes to find prime numbers.

2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
All even numbers are divisble by 2. If the sum of the digits of the number can be divided by 3 , the number is divisible by 3  .

 
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
If the last 2 digits of a number can be divided by 4, the number is divisible by 4.   

Example: 1  12 ÷ 4 = 28 and  12 ÷ 4 = 3

 

 If a number ends in 0 or 5, it is divisible by 5. 
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
If a number can be divided by 2 and 3, it is divisible by 6. 

 

 These numbers are divisible by 7. 
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
These numbers are divisible by 8. If the sum of the digits of the number can be divided by 9 , the number is divisible by 9  .

Example: 54 ÷ 9 = 6    5 + 4 = 9

 

The first 27 prime numbers are shown here in yellow in the table below. 

2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
2 3 4 5 6 7
8 9 10 11 12 13
14 15 16 17 18 19
20 21 22 23 24 25
26 27 28 29 30 31
32 33 34 35 36 37
38 39 40 41 42 43
44 45 46 47 48 49
50 51 52 53 54 55
56 57 58 59 60 61
62 63 64 65 66 67
68 69 70 71 72 73
74 75 76 77 78 79
80 81 82 83 84 85
86 87 88 89 90 91
92 93 94 95 96 97
98 99 100 101 102 103
You can find these prime numbers by crossing out the multiples of 2, 3, 5 and 7 (except for themselves) on the chart.   

Practice these methods and then take Quiz 1 on Prime numbers.
Ps. Remember to use the checklist to keep track of your work.